生物大数据分析
6 . 转录组测序和分析
桂松涛 Blog
songtaogui@163.com

2024年11月
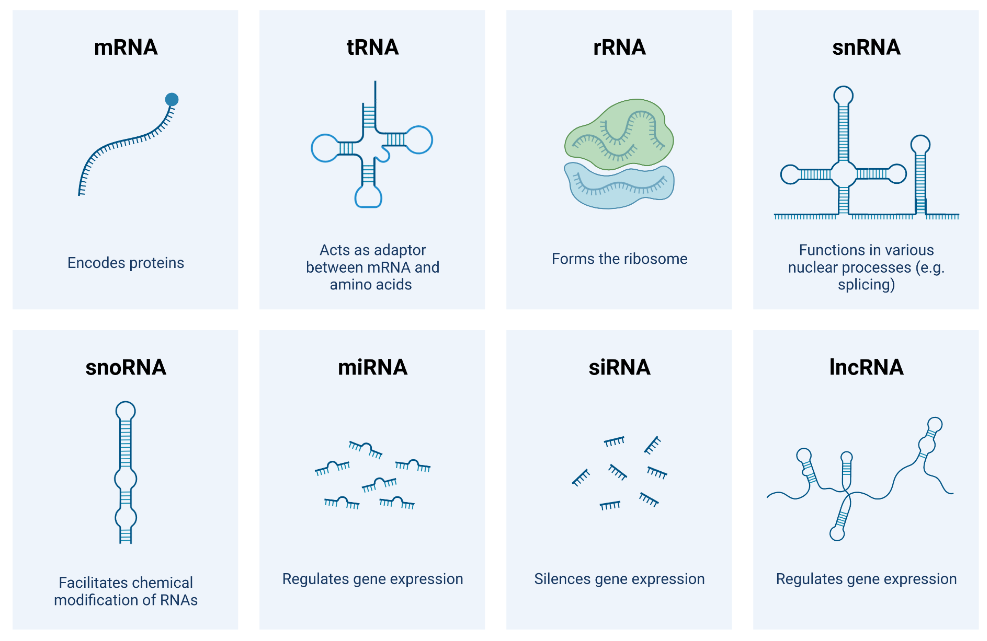
RNA和转录组
mRNA tRNA rRNA snRNA snoRNA miRNA siRNA lncRNA circosRNA ......
转录组研究
RNA-SEQ的挑战
RNA-SEQ分析内容和技术路线
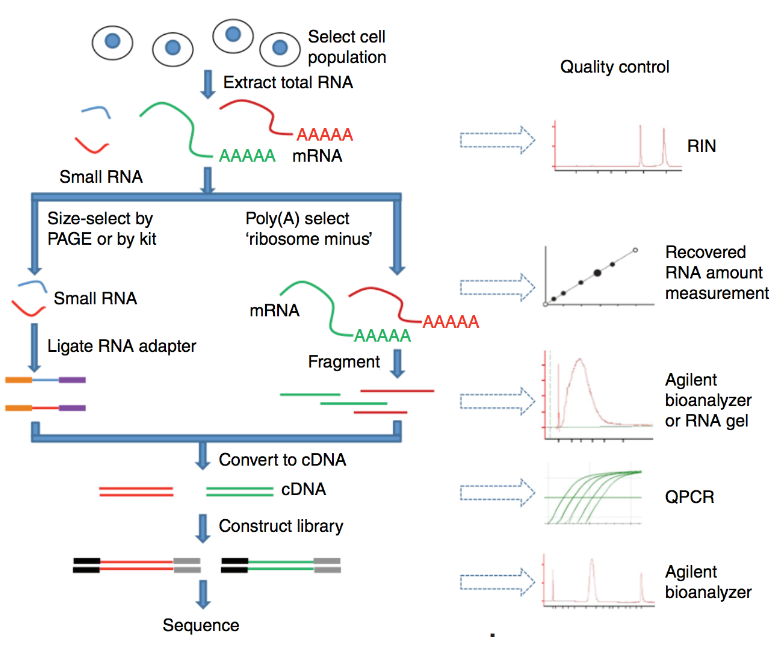
测序前的步骤
总RNA提取 RNA富集 RNA片段化 随机引物cDNA合成 测序接头
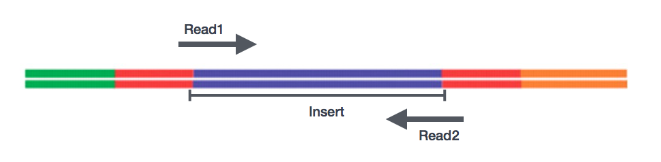
测序公司代劳
Sequencing Base calling
\( Q = -10 * log_{10}(P)\)
P: Base calling error probability
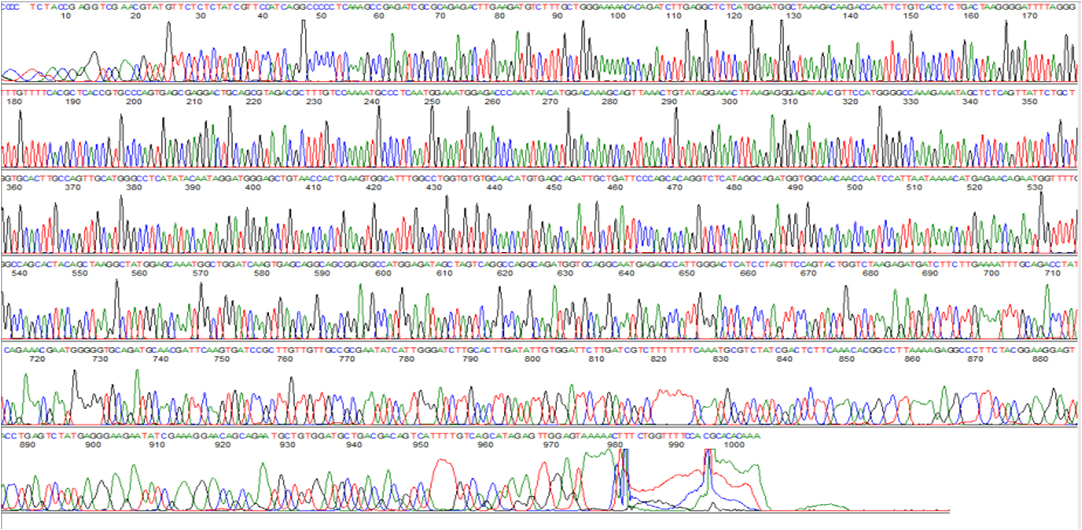
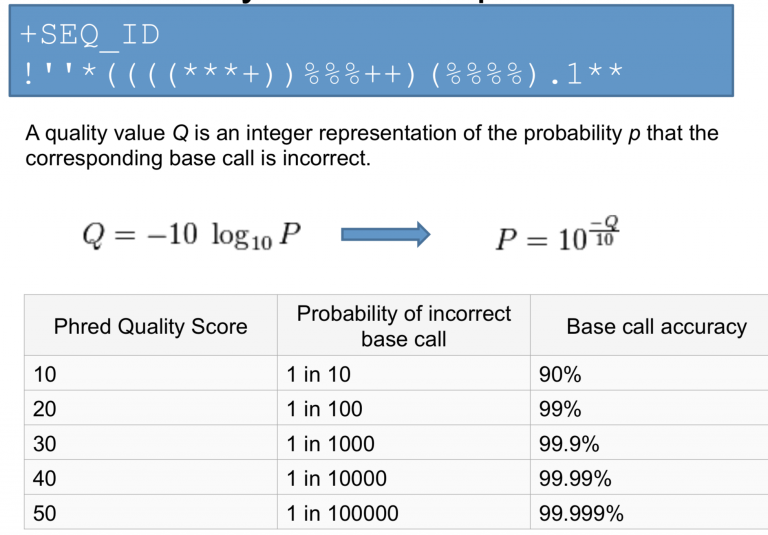
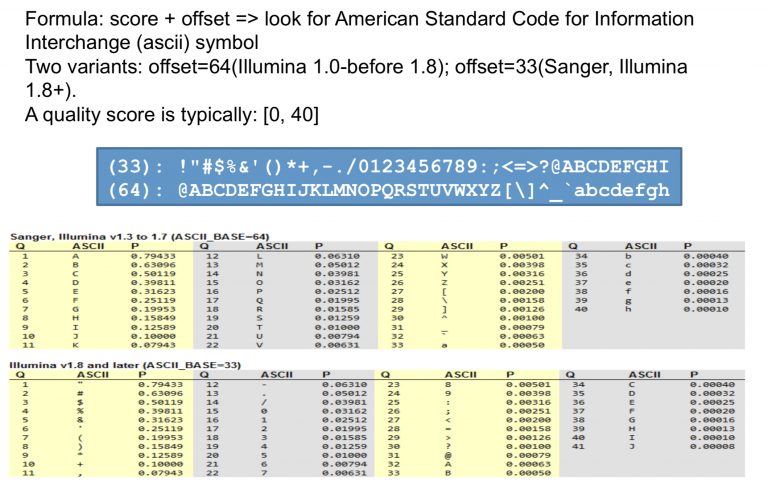
测序公司代劳
Sequencing Base calling De-multiplexing
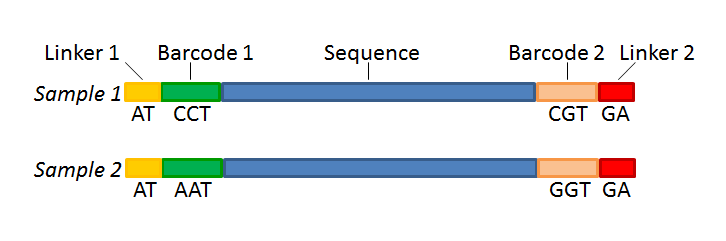
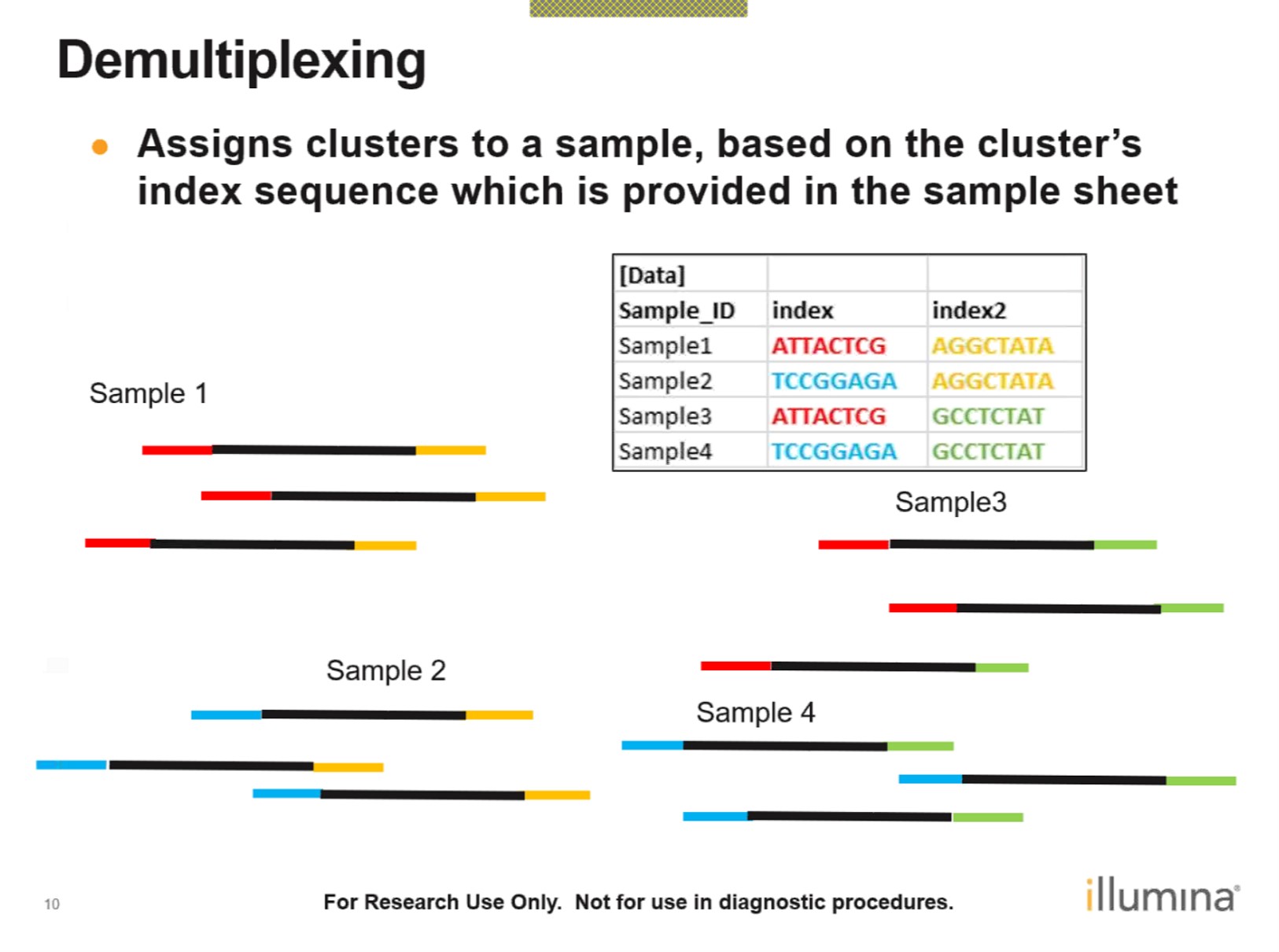
测序数据质量控制: FastQC
统计指标
描述
Number of Reads
reads数目
Data Size
碱基数量
N of fq1
reads1中N碱基数目
N of fq2
reads2中N碱基数目
Low qual base of fq1(<=15)
reads1中低质量的碱基数目
Low qual base of fq2(<=15)
reads2中低质量的碱基数目
Q20 of fq1
reads1中质量值>=20的碱基所占的比例
Q20 of fq2
reads2中质量值>=20的碱基所占的比例
Q30 of fq1
reads1中质量值>=30的碱基所占的比例
Q30 of fq2
reads2中质量值>=30的碱基所占的比例
GC of fq1
reads1的GC含量
GC of fq2
reads2的GC含量
Error of fq1
reads1的错误率
Error of fq2
reads2的错误率
Discard Reads related to N and low qual
N碱基和低质量的reads所占比例
Discard Reads related to Adapter
带接头的reads比例

FastQC: 质量值统计
Boxplot X: Base pair Y: Q score GOOD: 下四分卫数 > 30 WARN: 下四分卫数 < 10 or Median < 25 FAIL: 下四分卫数 < 5 or Median < 20
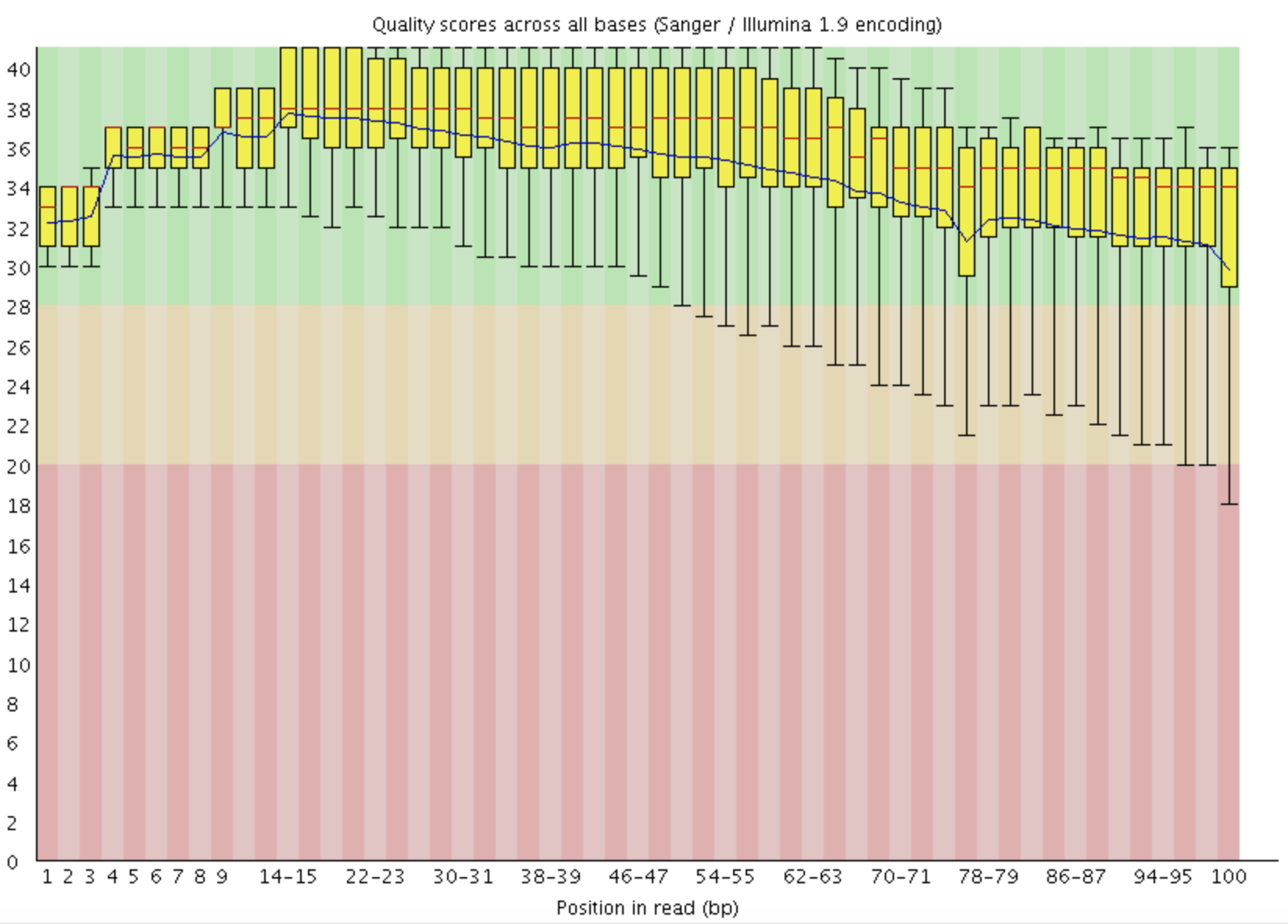
FastQC: 质量值统计 per sequence
Density Plot X: Mean Q score per reads Y: Number of reads GOOD: 90% reads has Q > 35 WARN: Peak < 27 (error rate > 0.2%) FAIL: Peak < 20 (error rate > 1%)
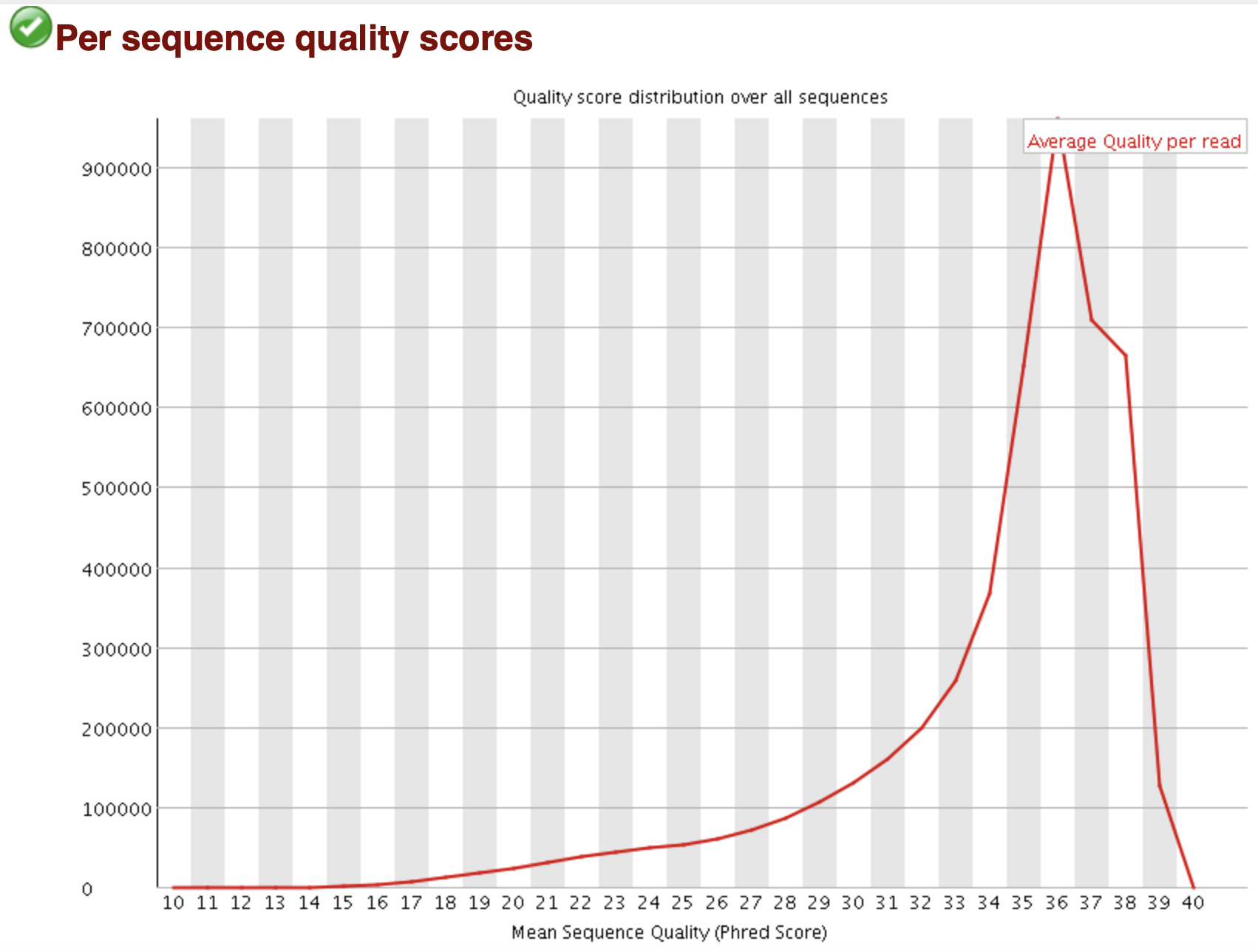
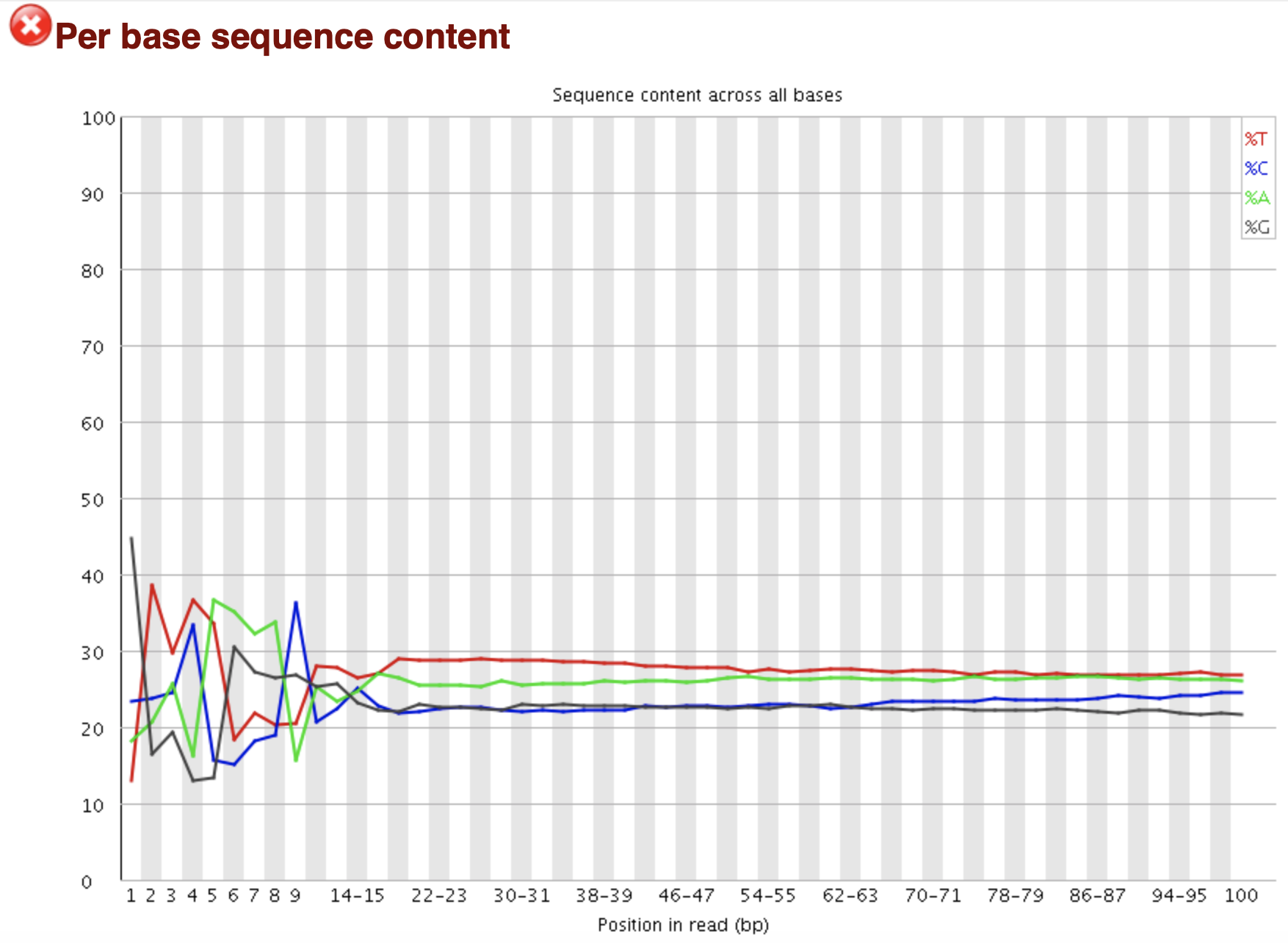
FastQC: 序列组成统计 per sequence
Line Plot X: Base pair Y: Percentage 随机文库中,理论上四种碱基出现概率相当 平行但分开的线: 文库bias或测序系统误差 WARN: 任一位置的A/T vs G/C相差 > 10% FAIL: 任一位置的A/T vs G/C相差 > 20%
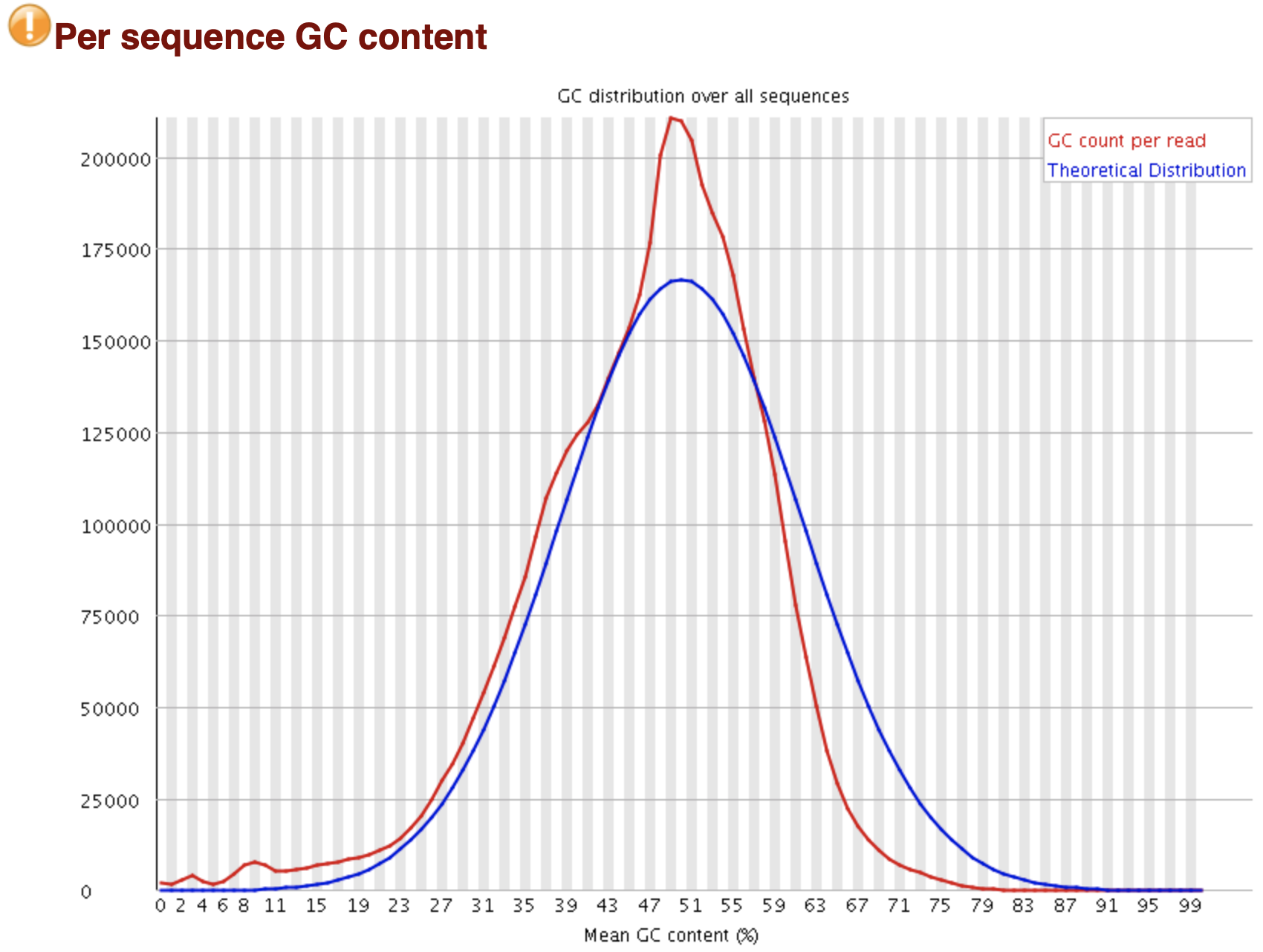
FastQC: GC含量分布 per sequence
Line Plot X: Mean GC Content (%) Y: Reads count cnote{蓝线}: 理论分布(正态分布) cerror{红线}: 实际分布 形状偏离正态分布: 文库污染、reads代表性有偏... 形状接近正态,但偏离理论分布: 系统误差 WARN: 偏离理论分布的reads > 15% FAIL: 偏离理论分布的reads > 30%
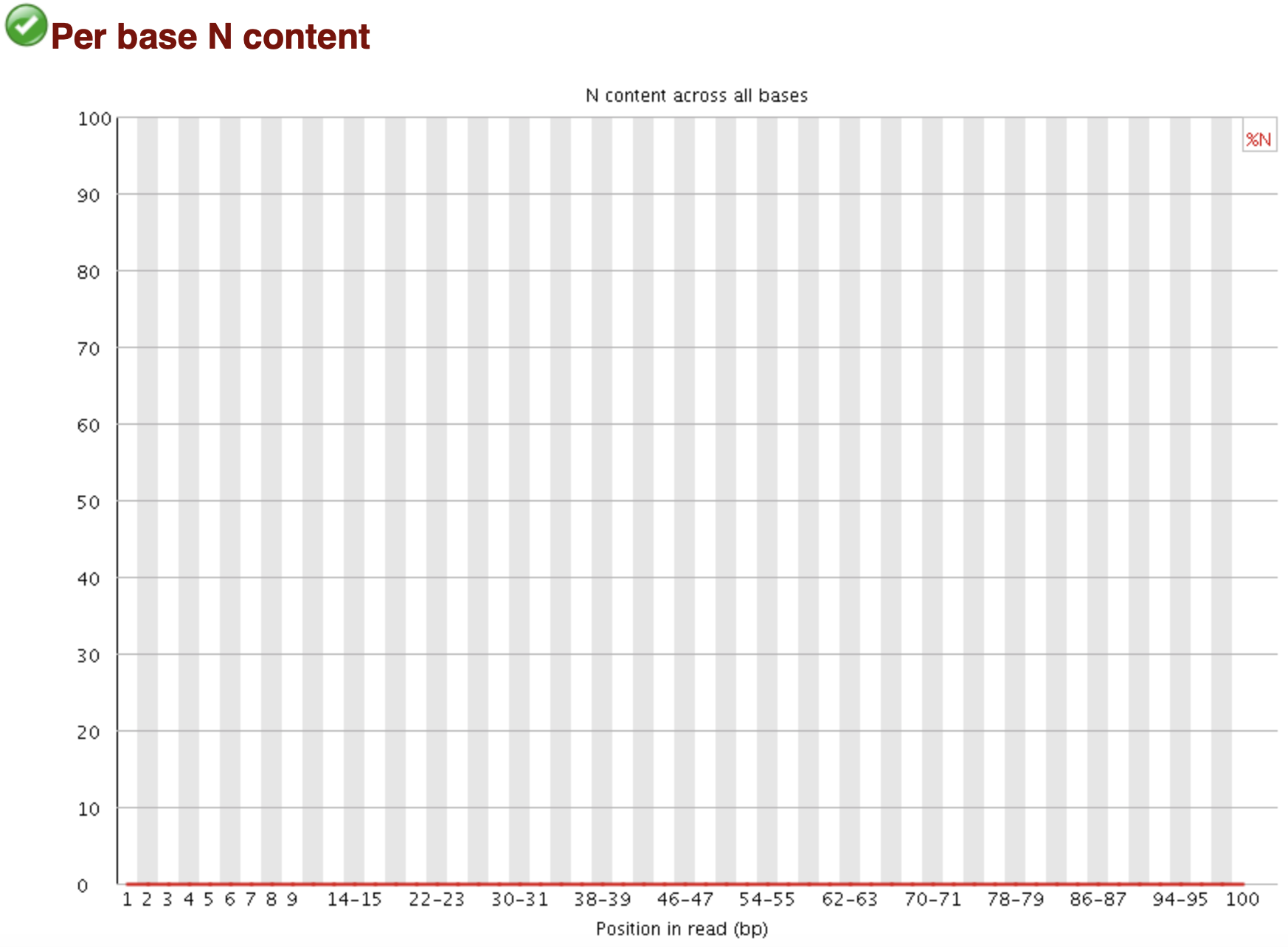
FastQC: N碱基分布 per sequence
Line Plot X: BP Y: Percentage of N 正常情况下N的比例很小: 紧贴X轴的水平线 "鼓包": 测序系统问题 WARN: 当任意位置的N的比例超过5% FAIL: 当任意位置的N的比例超过20%
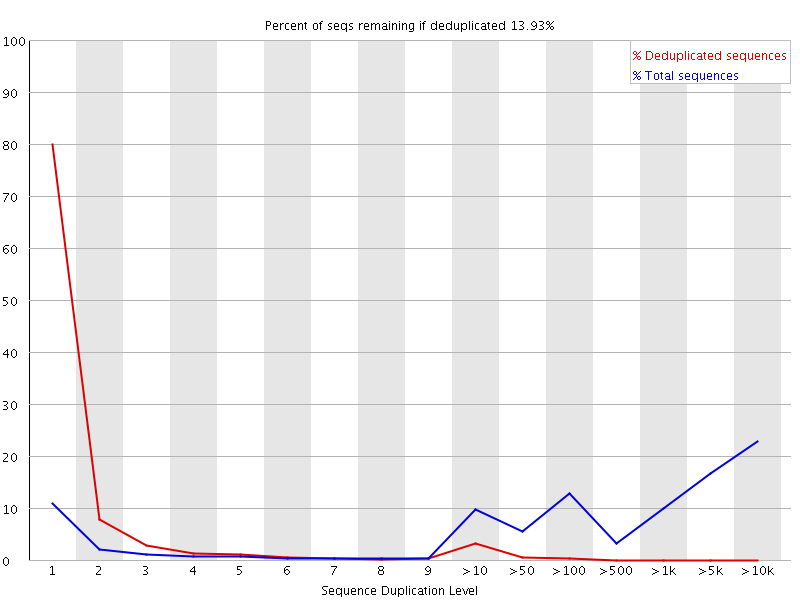
FastQC: 重复序列比例
Line Plot X: Sequence Duplication Level Y: Reads percentage 建库过程会产生重复, 测序本身也会产生重复; WARN: 当非unique的reads占总数的比例大于20%时,报"WARN"; FAIL: 当非unique的reads占总数的比例大于50%时,报"FAIL“。
FastQC: 完全一样的reads频率
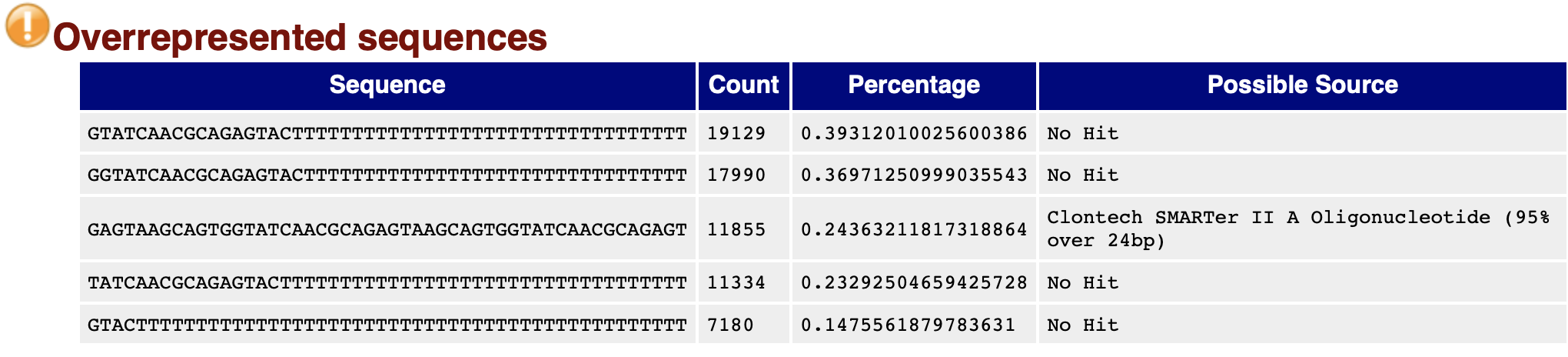
输出在总reads中出现次数超过0.1%的reads;
大量高比例的reads可能表示测序污染;
FastQC: 接头序列含量
Adapter序列在reads中出现的概率 WGS测序中不太会测到接头(片段长) RNA-Seq中有短序列,有可能测到接头 "鼓包": 测序系统问题 WARN: > 5% FAIL: > 10%
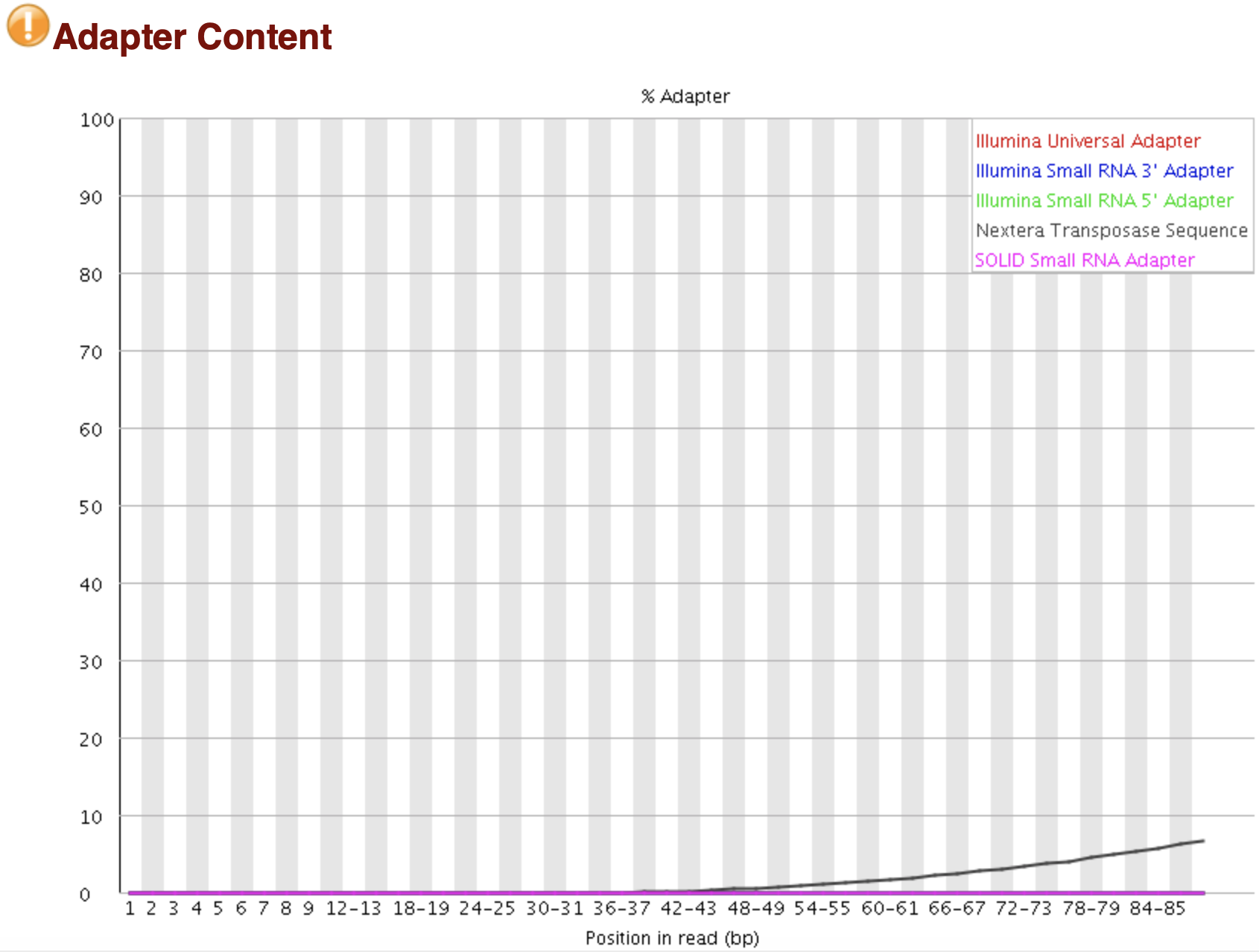
数据清洗: Trimming
去除Adapter序列 去除序列两端低质量碱基 删除低质量的reads 删除长度过短的reads
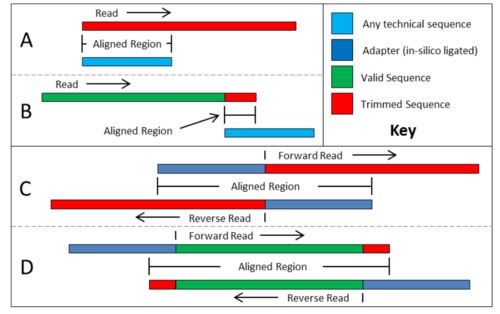
序列比对: WGS Mapping
序列联配 计分矩阵 Gap罚分 动态规划 序列索引(FM-index) ...
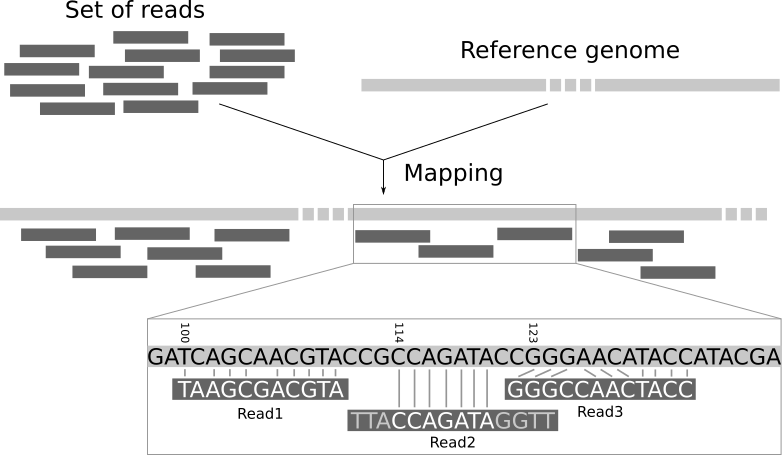

序列比对: RNA-Seq Mapping
常用的RNA-Seq比对软件:
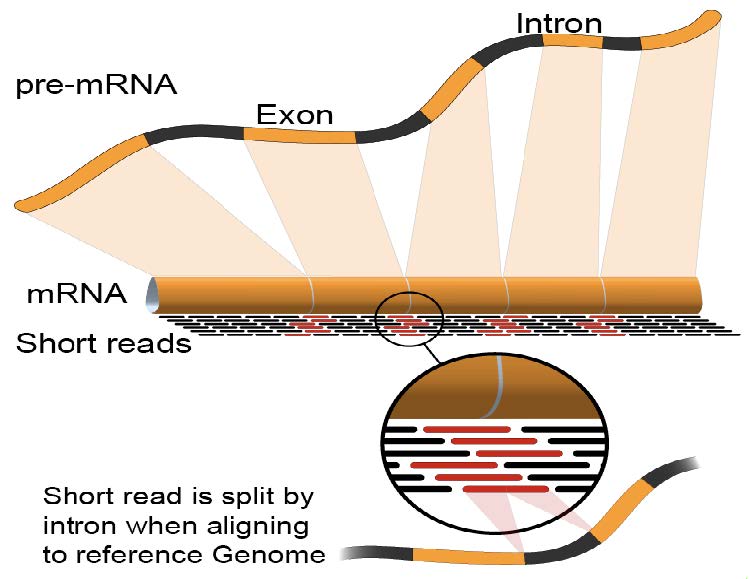
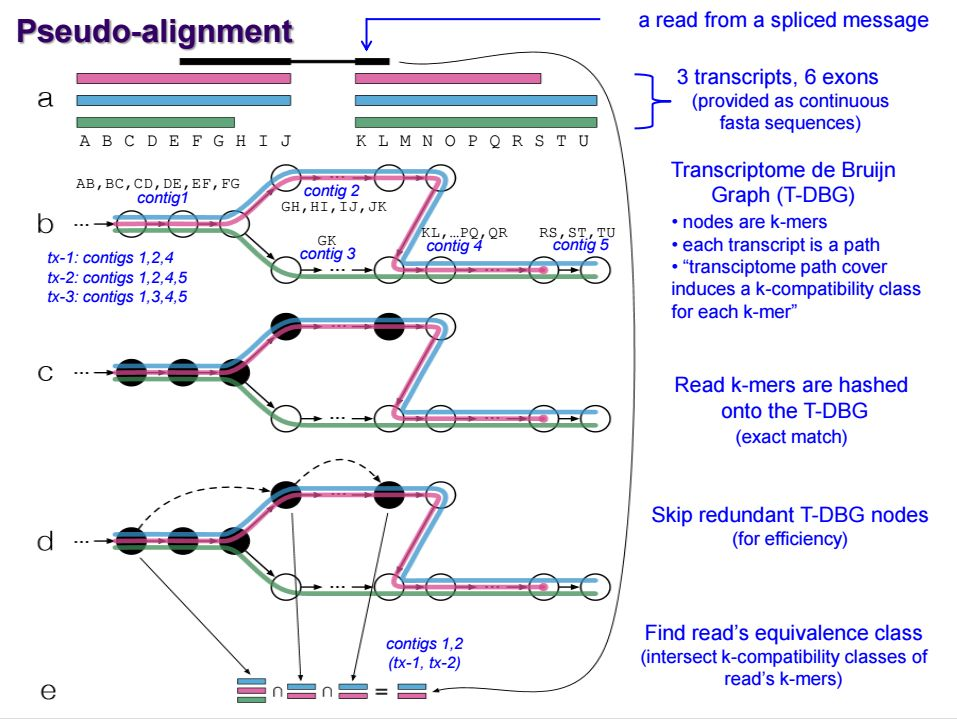
Alignment Free quantification
Kmer based Ultra Fast
无参转录本分析: 转录本组装
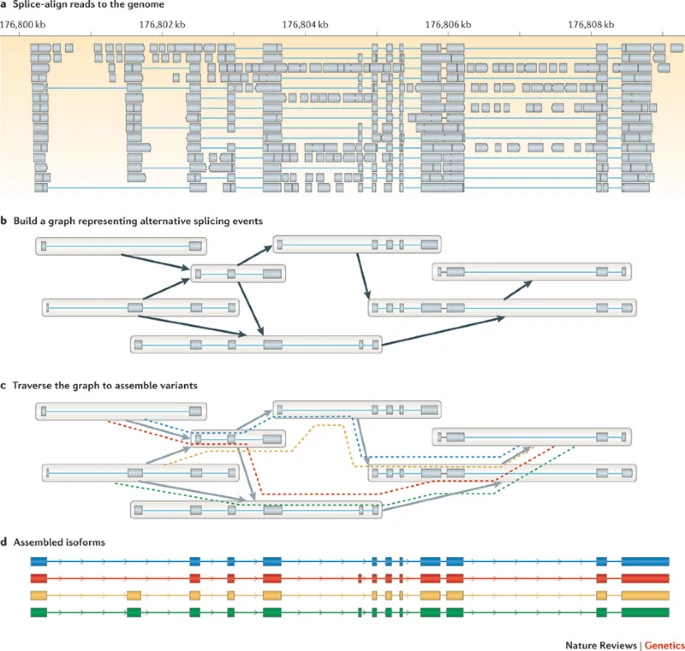
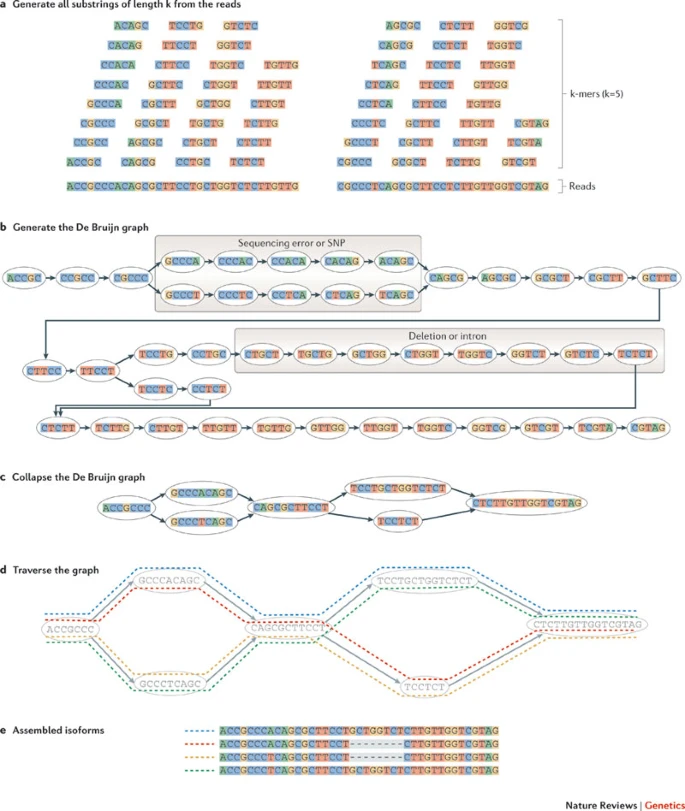
转录本定量: 计数
|
|
转录本定量: 计数
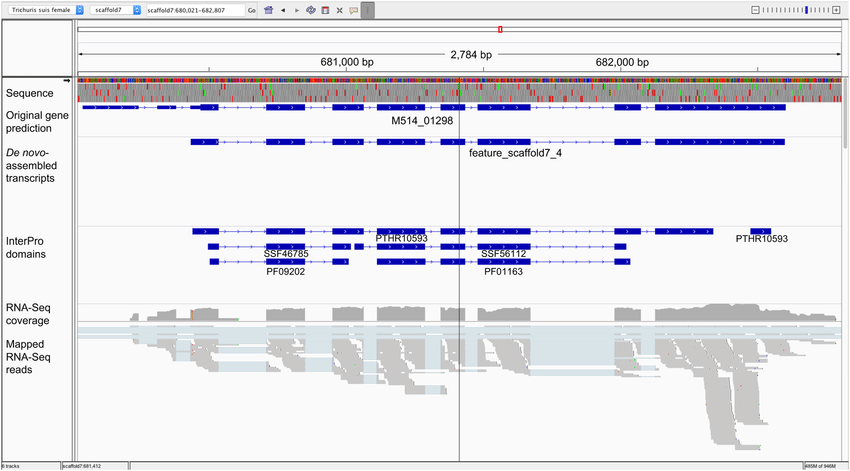
转录本定量: 标准化
|
RNA-Seq Reads Count的标准化
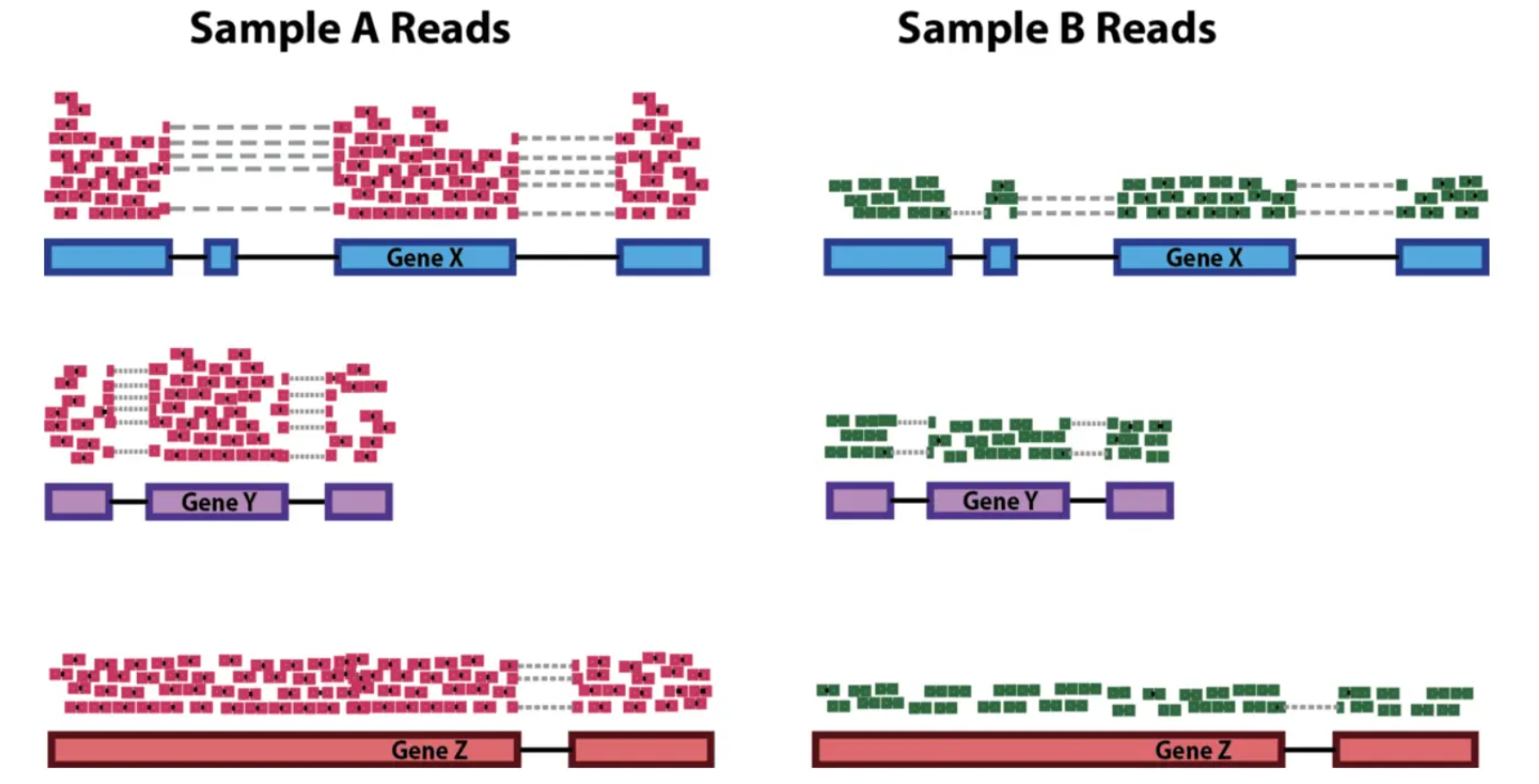 |
\( CPM = \frac{A * 1E6}{G} \) \( RPKM/FPKM = \frac{A * 1E6}{G * L_A / 1000} \) \( TPM = \frac{RPK_A * 1E6}{\sum{(RPK_A)}} \quad where \quad RPK_A = \frac{A}{L_A / 1000}\) |
转录本定量: 过滤低表达基因
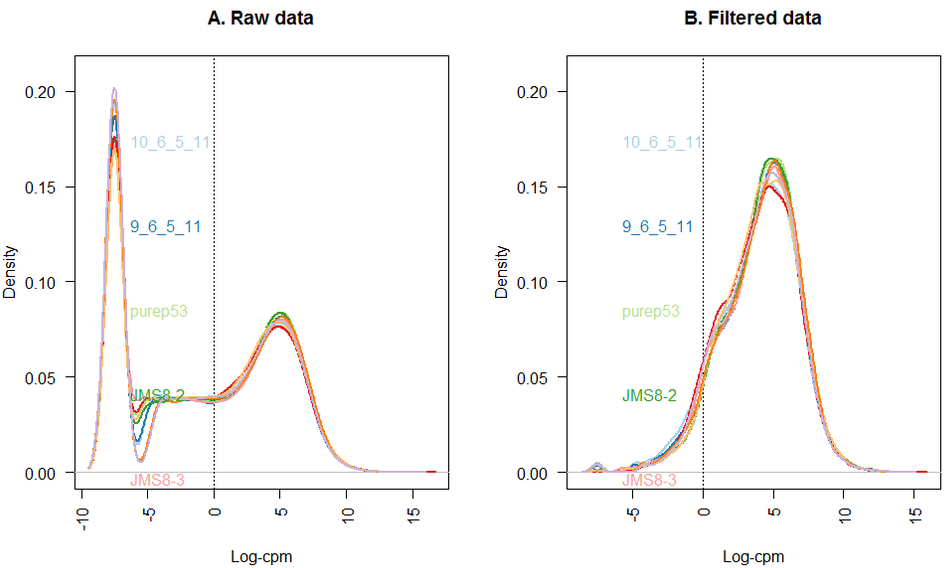
转录本定量: 其他标准化方法
管家基因 Spike-in: 建库时添加绝对定量内参 TCS (Total Count Scaling) \( x^p_i = d_i x_i \) Quantile: 排序后求平均再回序

转录本定量: 其他标准化方法
Median of Ratio (DESeq2) 对每个基因计算几何平均数 比较每个样本每个基因和参考样本的Fold Change 用Fold Change 中位数基因代表内参基因进行标准化 TMM: Trimmed Mean of M value (EdgeR) 移除未表达的基因 找数据趋势较为平均的样本当参考样本(依据Q3值) 计算基因偏倚度:LFC (log fold change)和read的几何平均数 (read geometric mean, RGM) 依据LFC和RGM挑选代表基因集, 计算标准化因子
样本质控: 数据整体分布的相似性
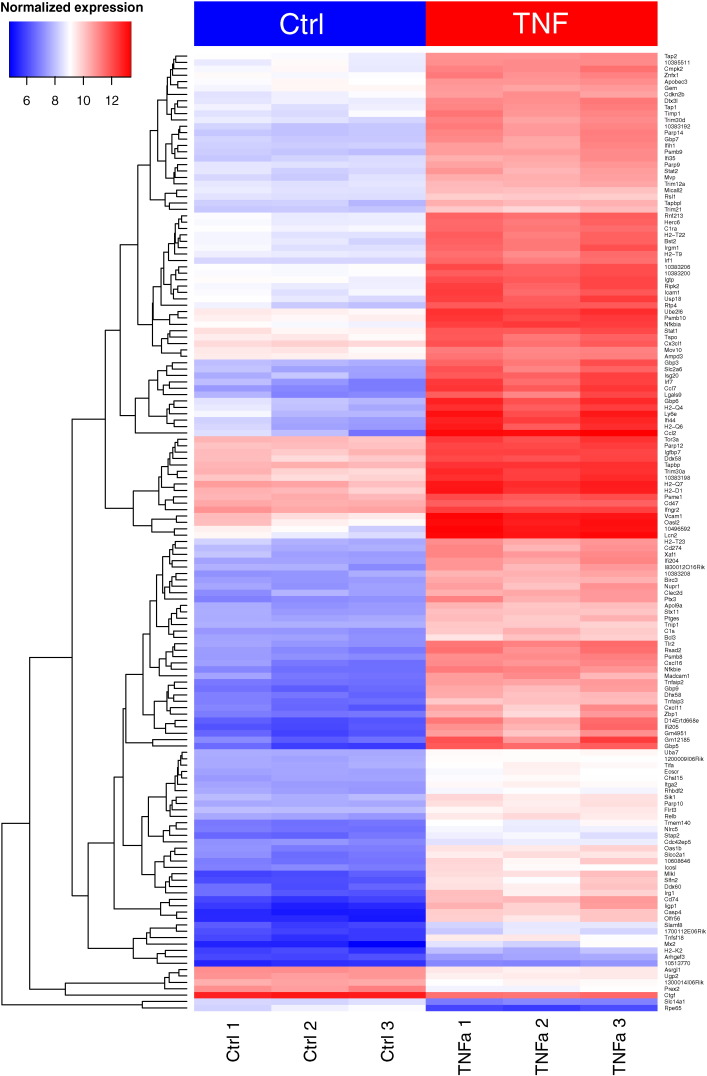
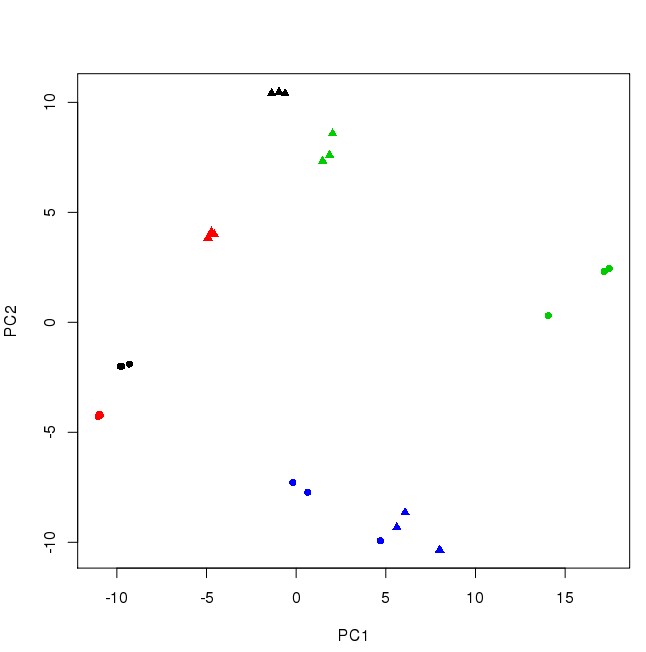
样本质控: 主成份分析
主成份分析(Principal components analysis, PCA)是很经典的降维算法,可用来降噪、消除冗余信息等。
|
极端例子:Y轴数据提供信息量少,可以直接舍弃
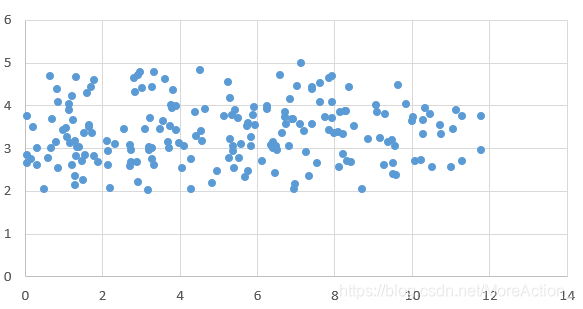 |
一般情况: X&Y信息变化大,需要通过降维算法进行计算
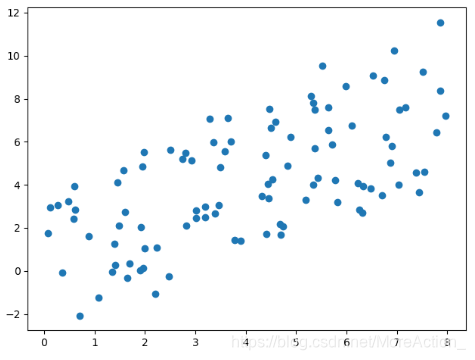 |
|
|
样本质控: 主成份分析
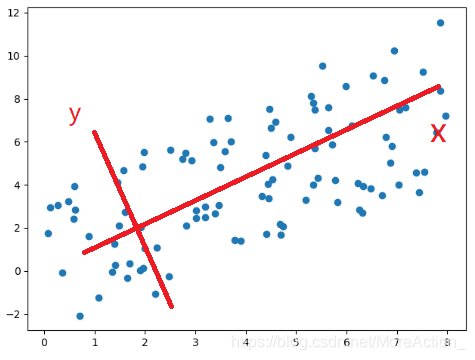
在新坐标系下,Y轴数据可以进行舍弃; 数据的具体数值不重要,重要的是分布(数据之间的关系); 降维的原理: 更改坐标轴(正交变换), 取新坐标轴上前K个变化最大的轴上的数据,实现N->K的降维; 深入理解的数学概念: 正交变换、正交矩阵、协方差、特征值分解、奇异值分解...
样本质控: PCA分析案例
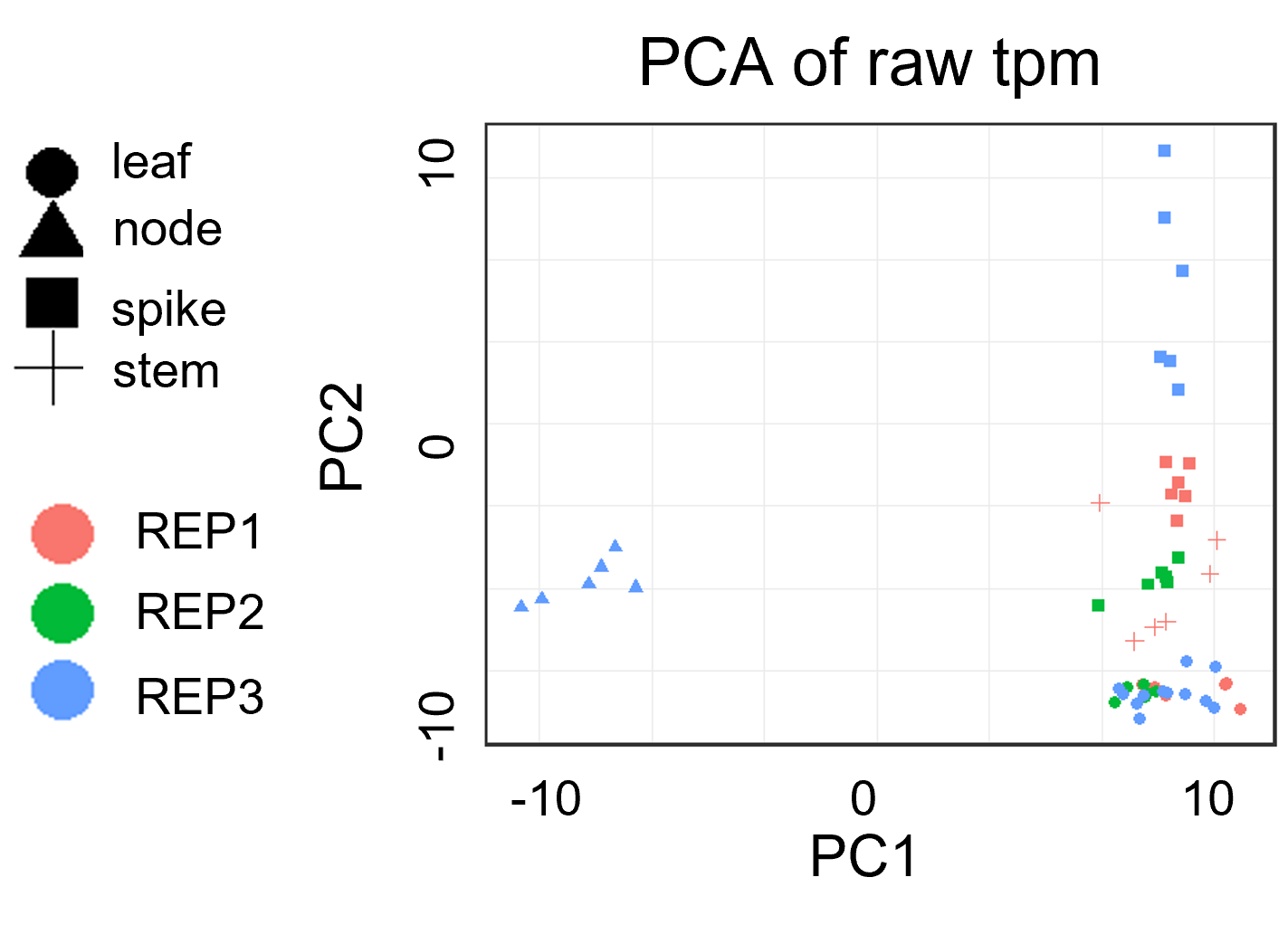
样本质控: PCA分析案例
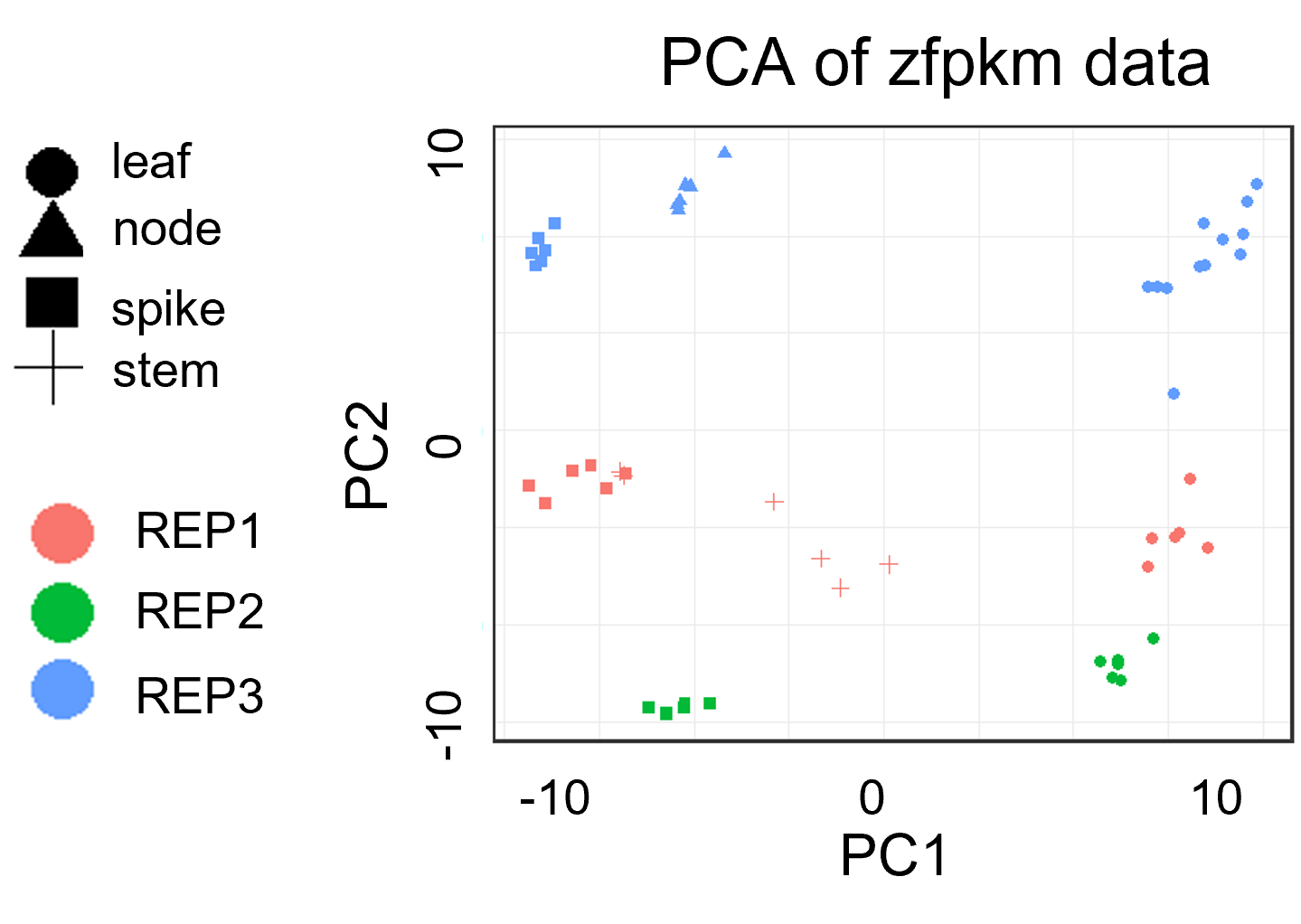
样本质控: PCA分析案例
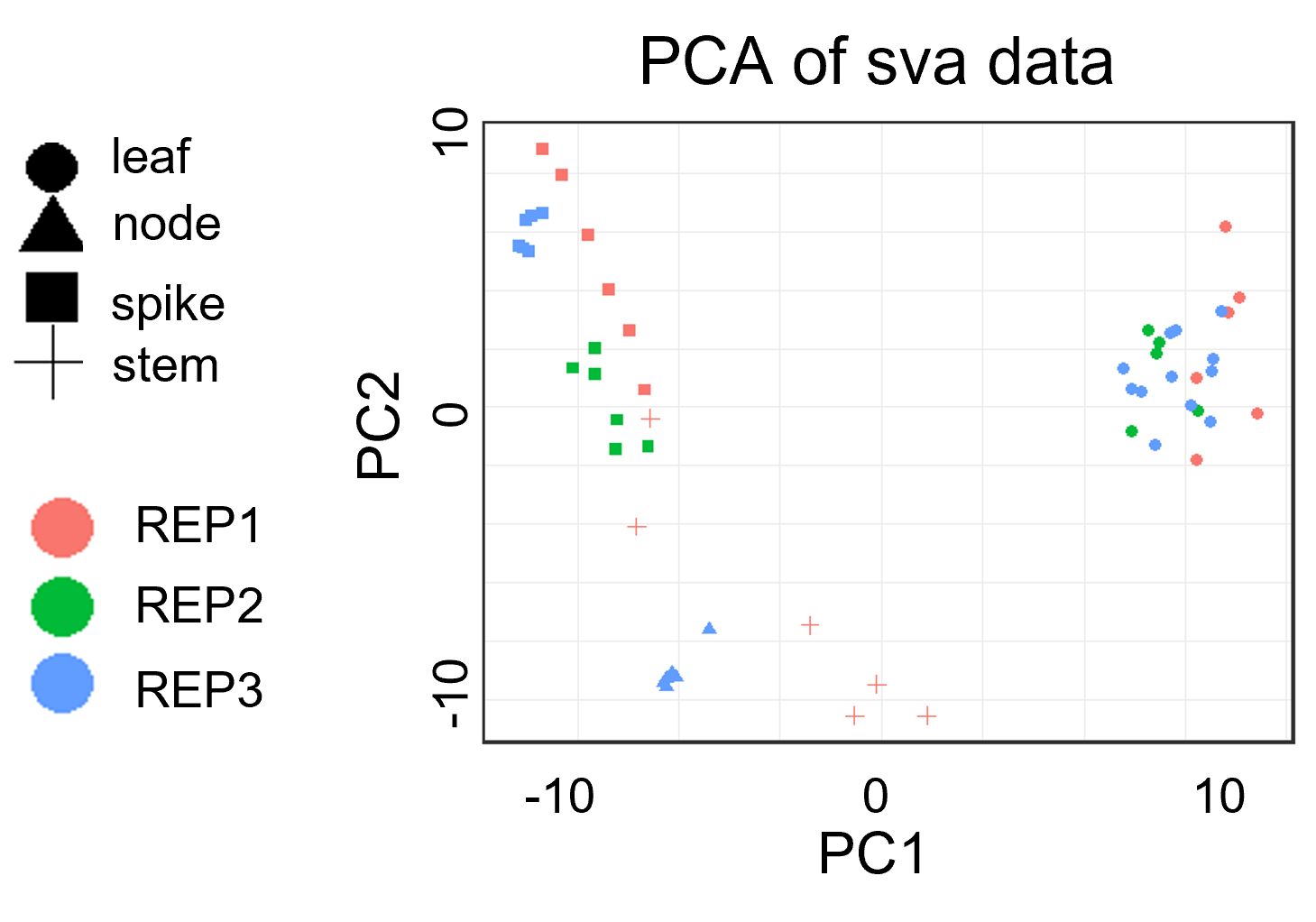
差异分析: 重复
生物学重复 vs 技术重复
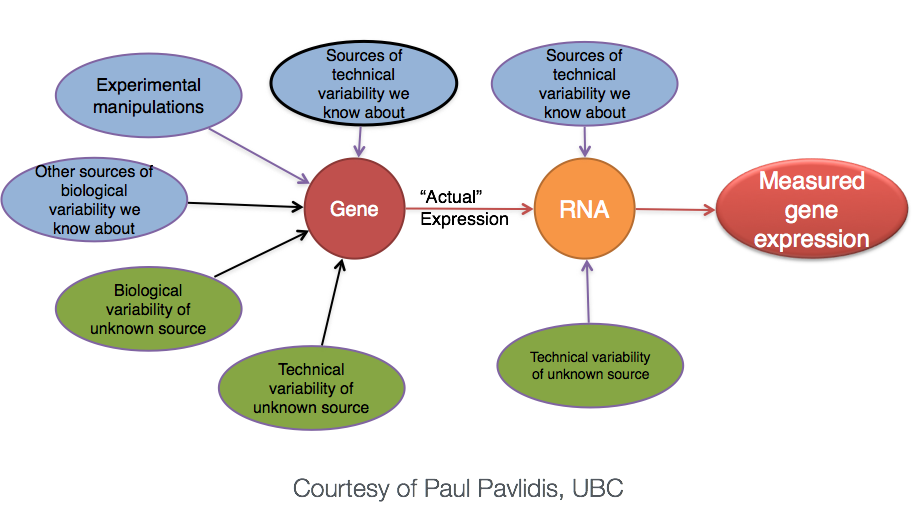
差异分析: 重复
重复越多,对总体均值和方差的估计越准确,越能得到更多DEG。
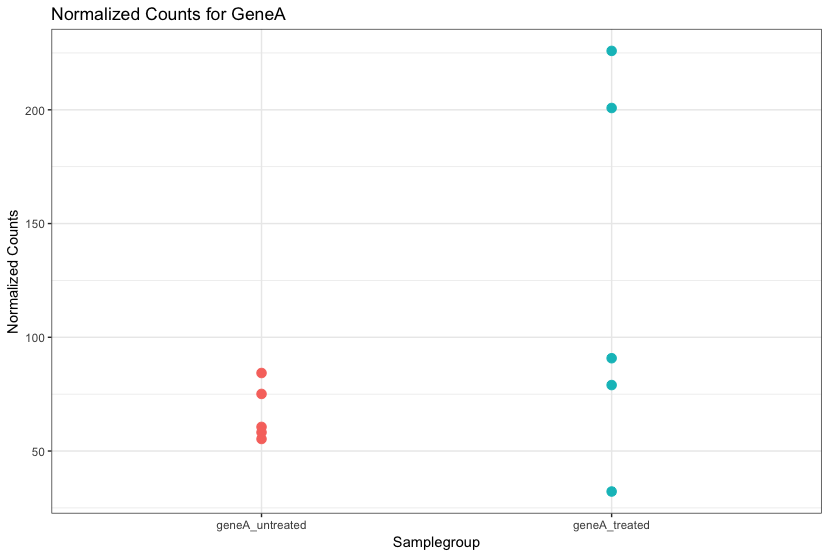
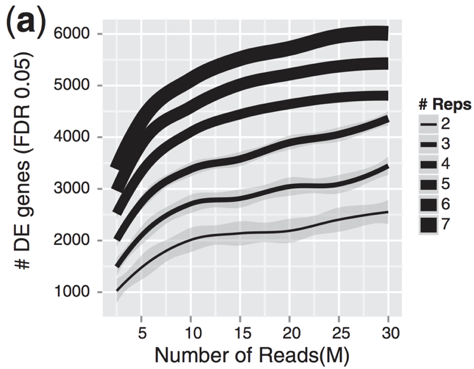
差异分析: 统计分布
传统数据的差异分析(多组: ANOVA):
|
|
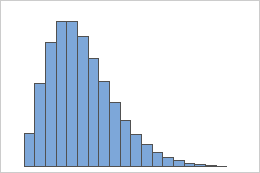
泊松分布? 负二项分布! Reads count是离散的非零整数, 对应的分布也是离散分布。
|
|||
|
|
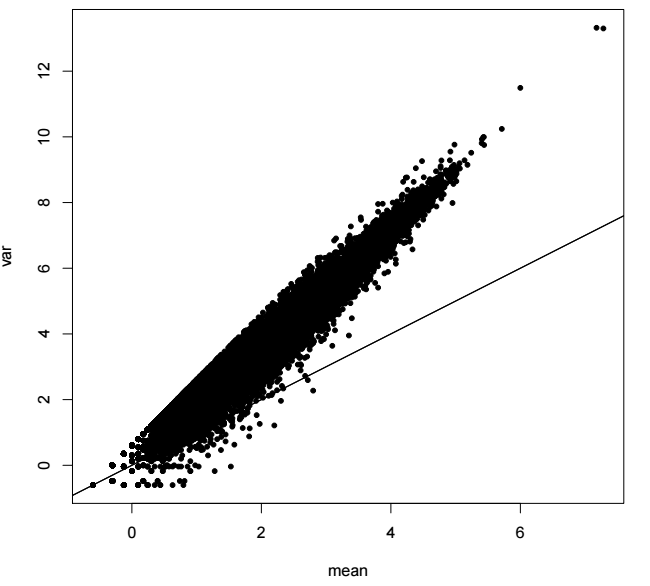
差异分析: 方差估计
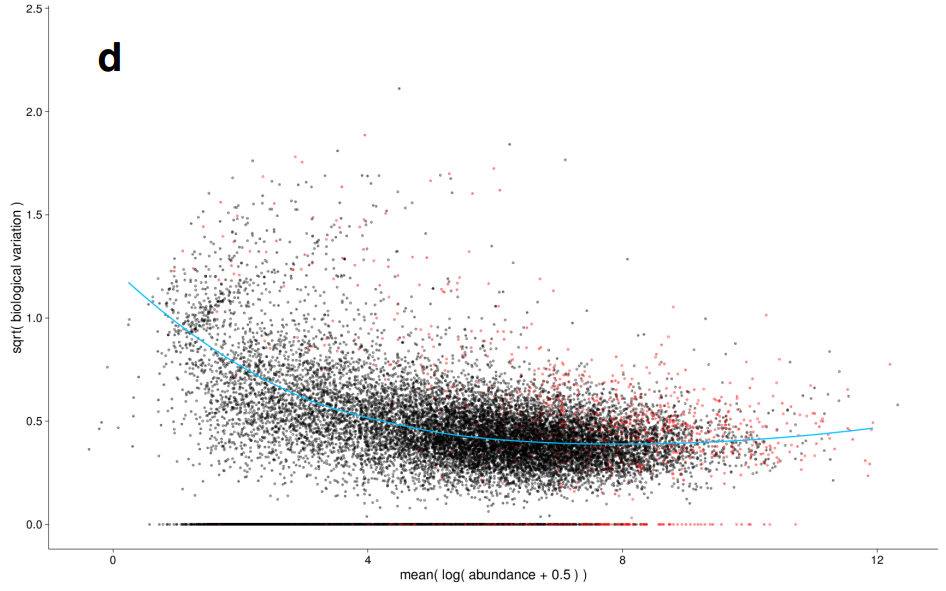
|
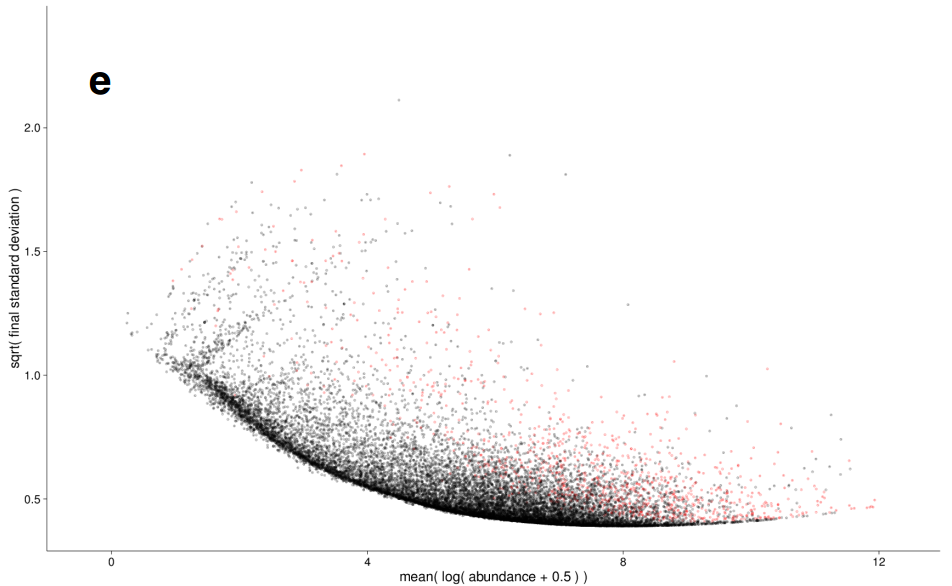
|
|
|
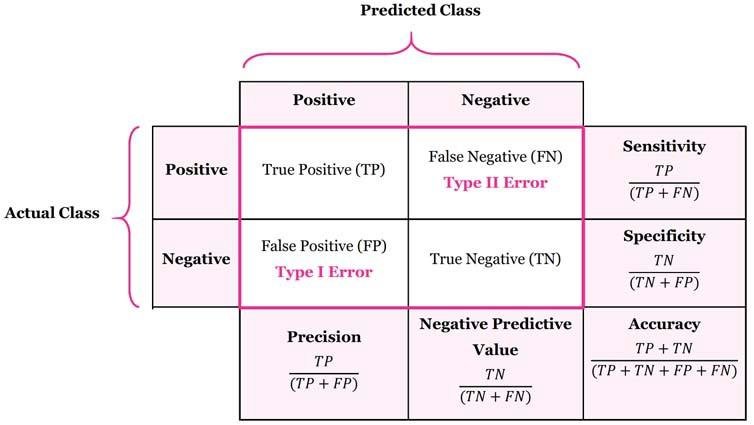
差异分析: 多重假设检验校正
\( H_0 \): You are not pregnant; \( H_1 \): You are pregnant
 |
 |
|
|
差异分析: 多重假设检验校正
差异基因分析:
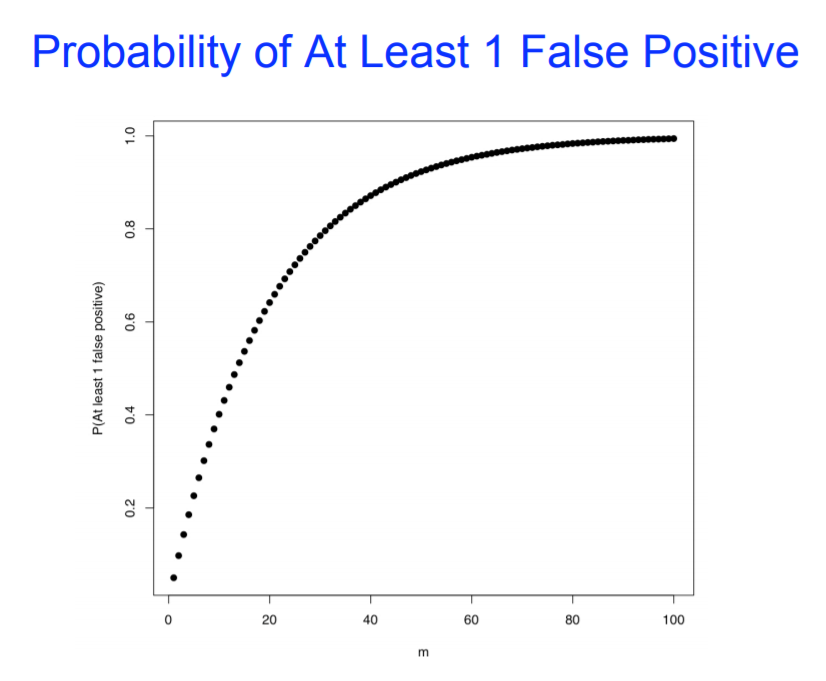
差异分析: 多重假设检验校正
如果多次假设检验的结果之间有影响,或需要将多次假设检验的结果合并分析,则需要校正。
例:寻找两种条件下具有差异表达的基因,我们会对每个基因在两组样本里的表达量分别进行检验(多重假设检验),但最后获得所有差异表达基因时需要将上述各结果合并,若不进行校正,则差异表达基因中假阳性结果就较多,故需要校正。
反之,如果多次假设检验的结果仅用来单独分析,不会将结果合并,则无需校正。
例:将基因分成几个基因集,比较这几个基因集之间某特征是否有显著差异,因两两之间的比较与其他基因集并无关联,故不需要校正。
差异分析: 多重假设检验校正常用方法
差异分析: 结果解读
Fold Change; P-value; P_adj/FDR/Q-value
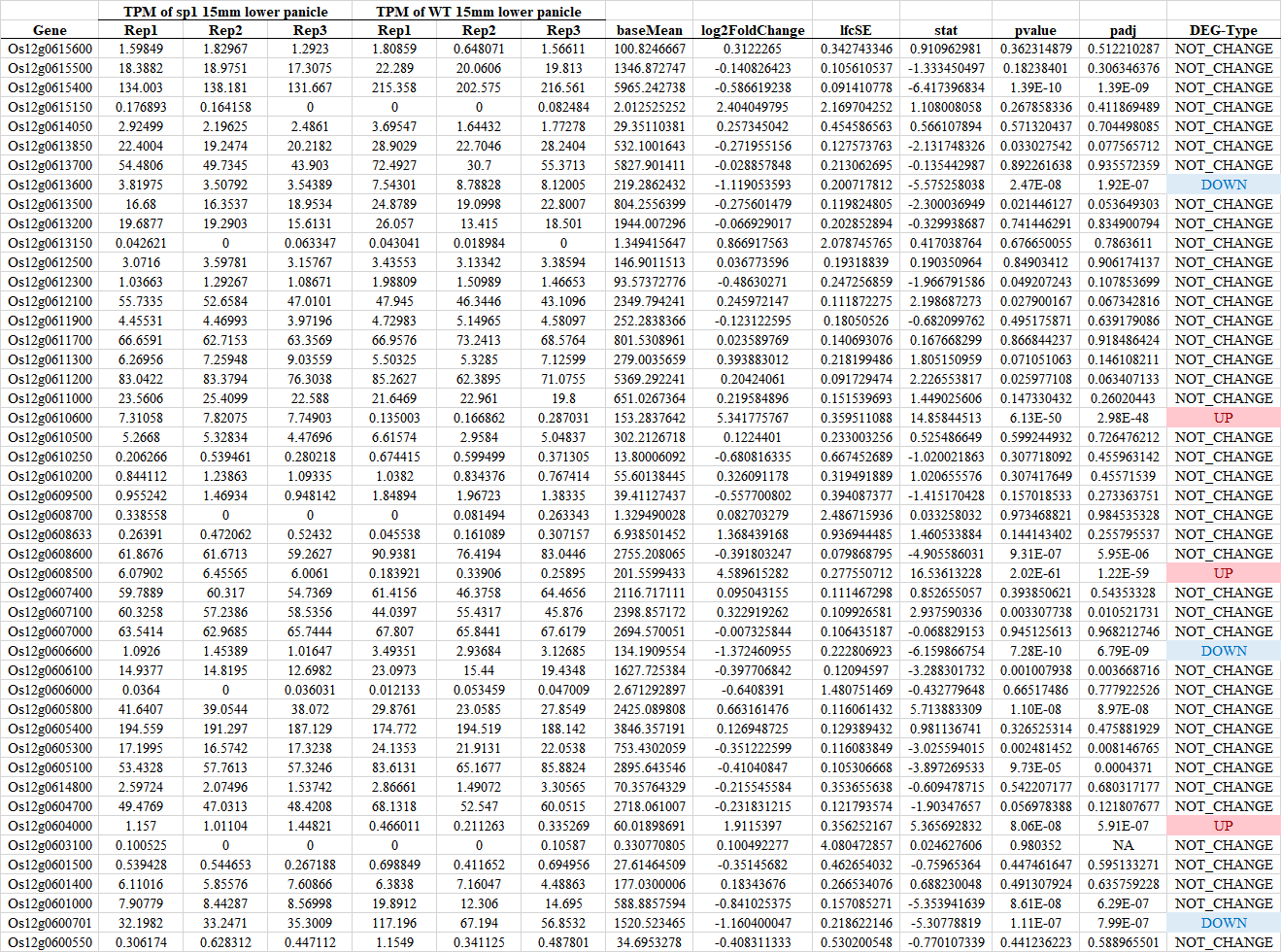
差异分析结果展示
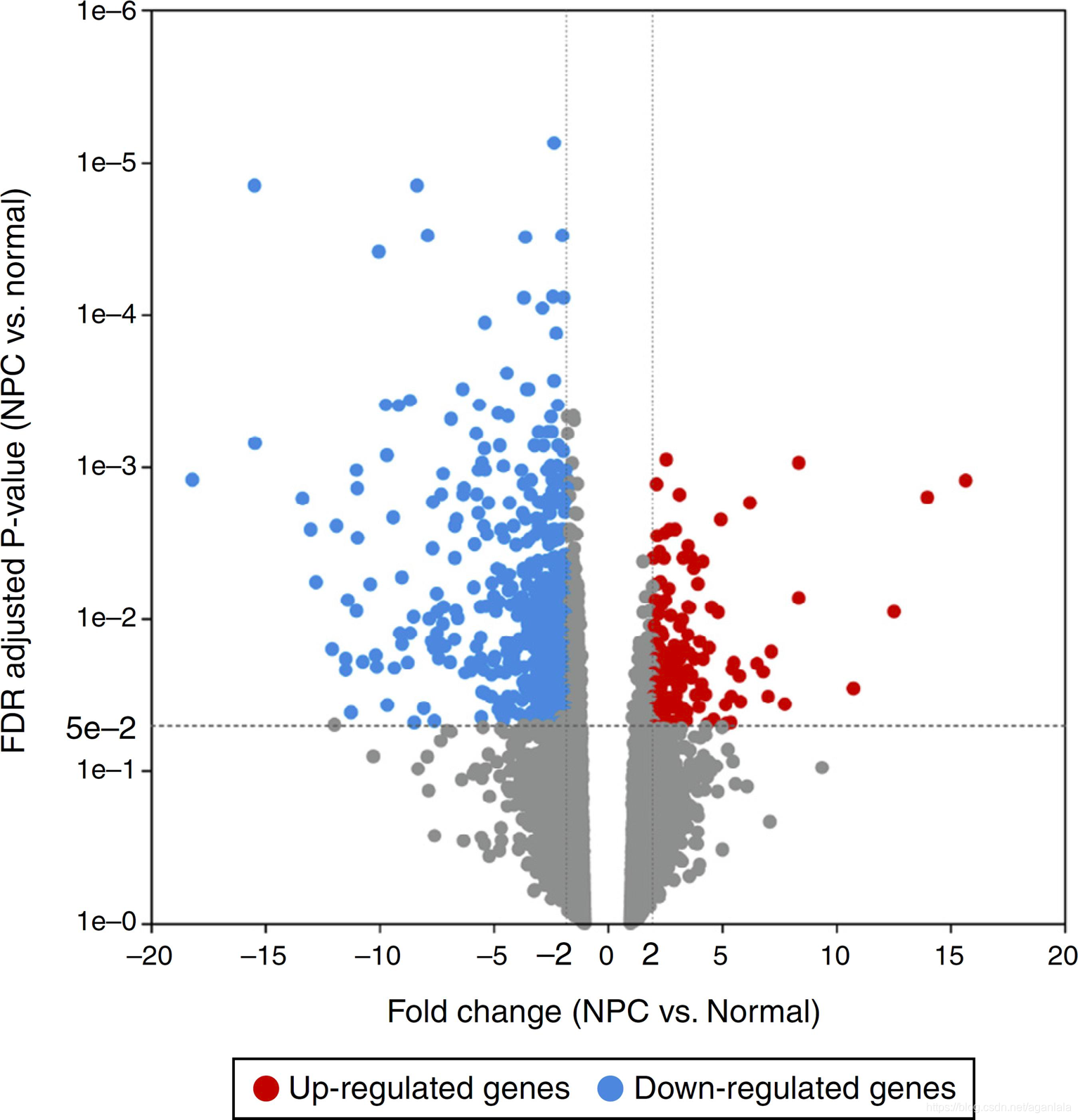
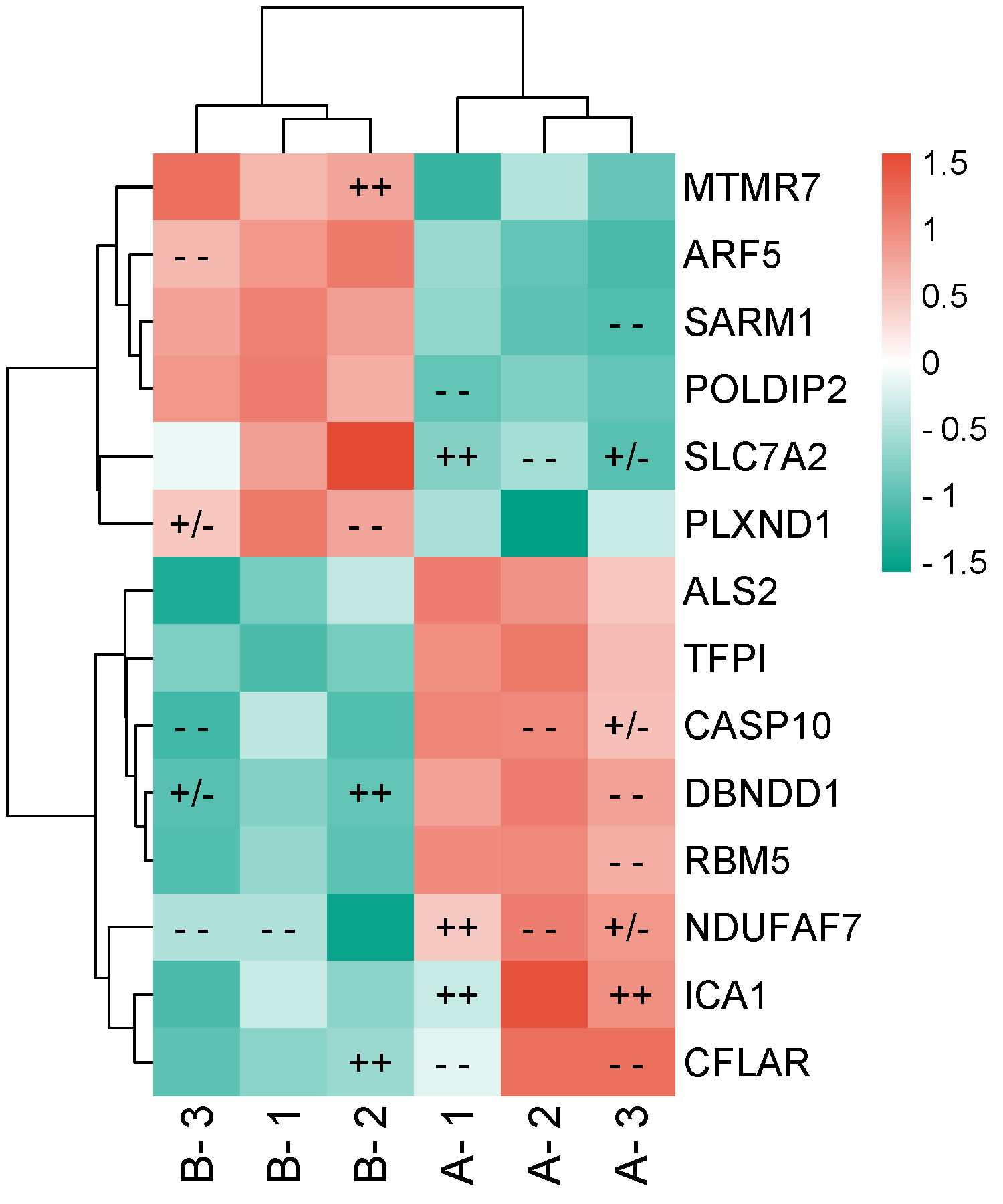
差异基因下游分析: 富集分析
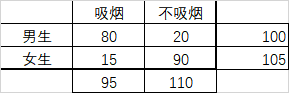
卡方检验
Fisher精确性检验
KS检验
差异基因下游分析: 富集分析
在 背景基因集(N) 下获得 一组特定基因集(S),
S可能是基因列表,表达图谱,基因芯片等形式。
用预先构建好基因注释数据库(例如GO,KEGG等)已对背景基因集(N)根据生物功能或过程进行分类
通过统计学算法找出有那些显著区别于背景基因集(N)的类别(生物组成/功能/过程)
或者找出这组特定基因集间在生物组成/功能/过程的共性
经过聚类后去除冗余得到基因富集结果的过程,即为富集分析。
差异基因下游分析: 富集分析
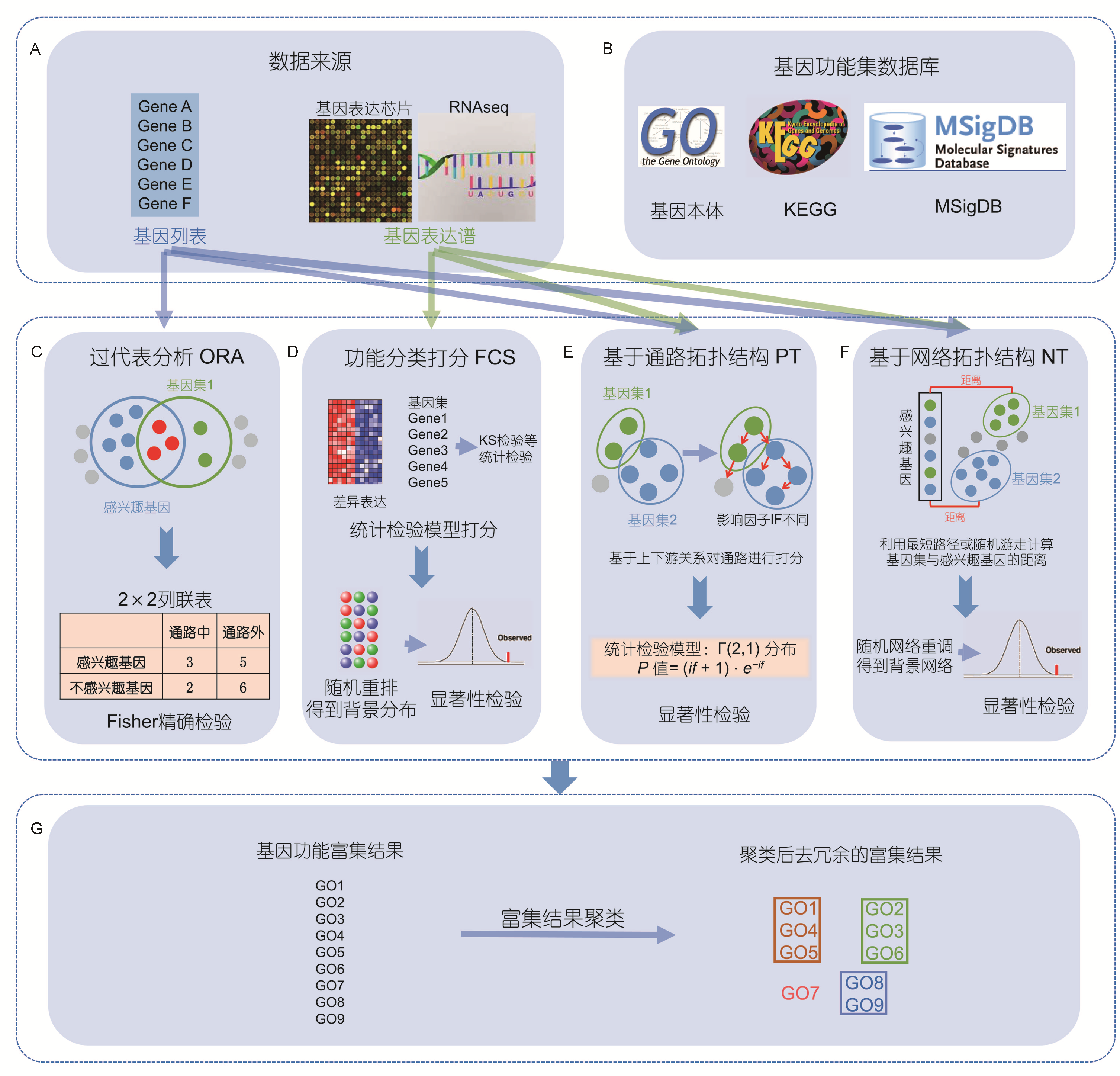
差异基因下游分析: 富集分析 -> 基因本体论(Gene ontology, GO)
单个的基因产物(包括蛋白质和RNA)或多个基因产物的复合物在分子水平上的活动,比如“催化”,“转运” 需要注意,这里的描述只表示活动,而不指定执行功能的实体(分子或复合物),动作发生的地点,时间或背景 基因产物在执行功能时所处的细胞结构位置,比如在线粒体,核糖体 需要注意:细胞组分是细胞解刨结构,不指代过程 通过多种分子活动完成的生物学过程 需要注意:生物学过程不等同于通路。目前,GO没有表示完整的通路信息所需的动力学或依赖性的描述信息
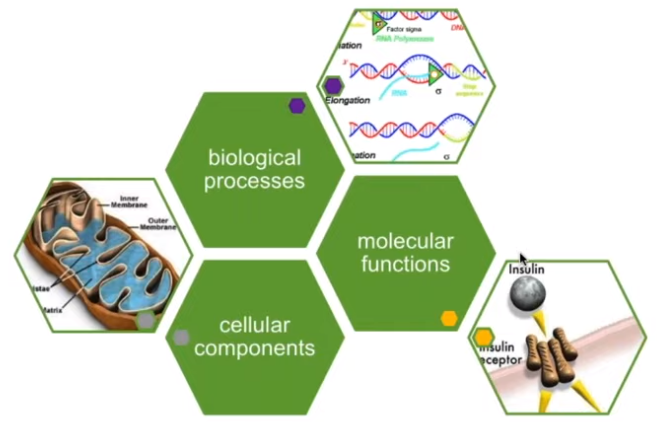
GO 富集结果示例
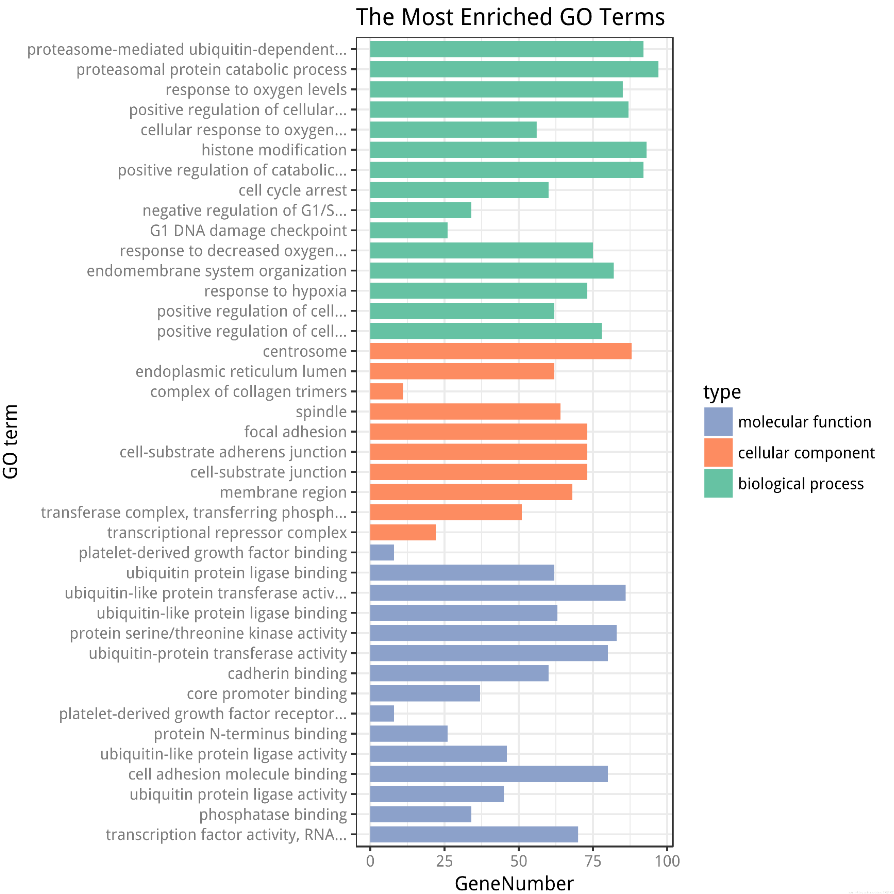
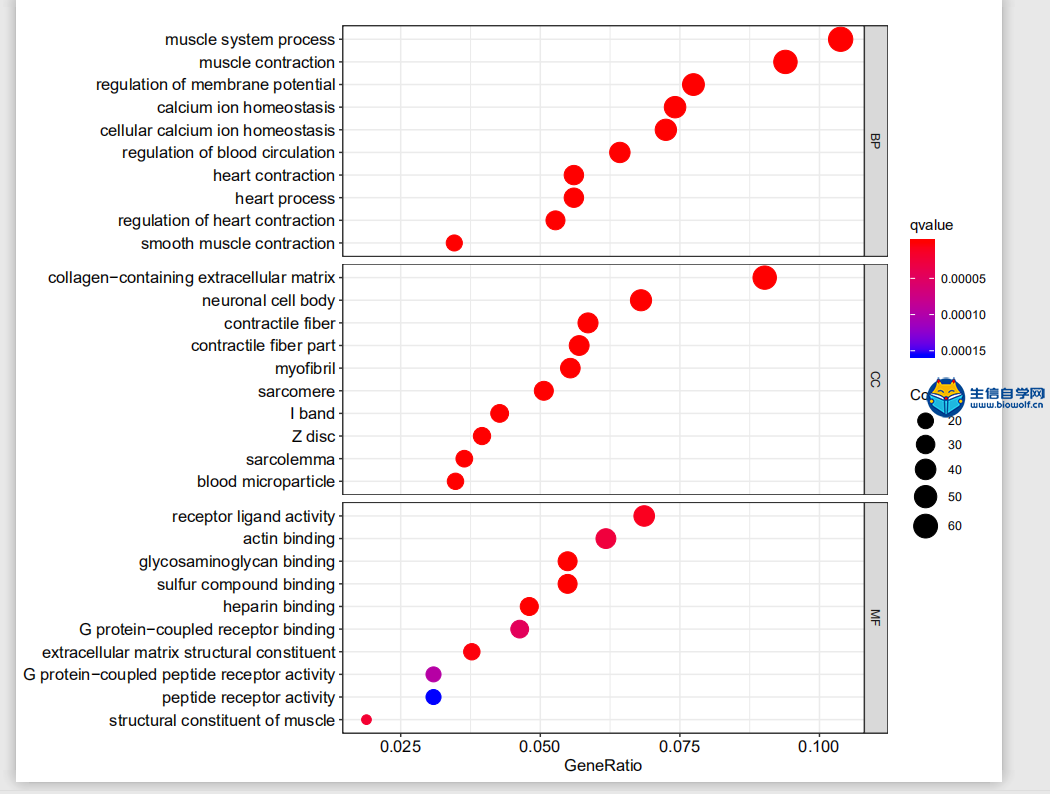
RNA-Seq分析实操流程
nf-core/rnaseq: https://github.com/nf-core/rnaseq