生物信息学

2.1 生物信息学中的统计知识概览



桂松涛 Blog
songtaogui@163.com

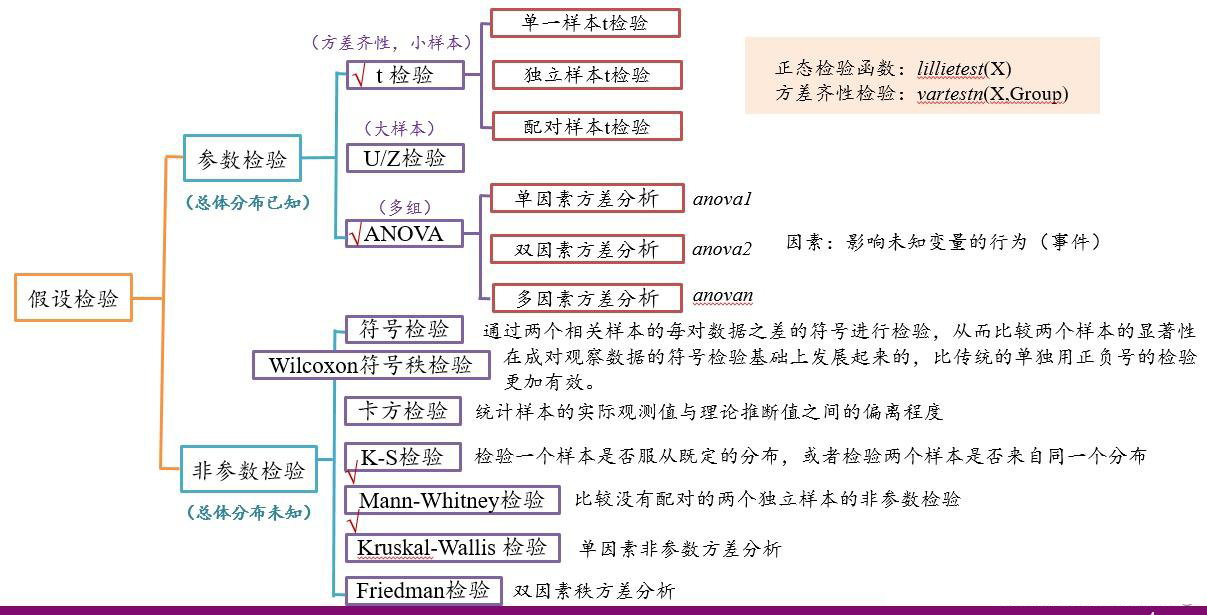
统计方法导览


数据基本描述

  • 集中趋势: mean, median, mode

  • 离散程度: sd(\(σ\)), variance, cv, quartile

  • 分布形态: 偏度(skewness), 峰度(Kurtosis)


数据清洗

  • 缺失值的处理

  • 异常值的处理

  • 数据缩放转换


数据分布检验

  • 正态分布

  • 方差齐性分布

  • 二项分布

  • ...
差异分析

  • 计量变量 参数检验

    • t检验

    • 单因素方差分析

  • 计量变量 非参数检验

    • wilcoxon符号秩和检验

    • Kruskal-Wallis H检验

    • Fridman M检验

  • 分级变量

    • wilcoxon符号秩和检验

    • Kruskal-Wallis H检验

    • Jonckheere-Terpstra检验

  • 计数变量

    • 卡方检验

    • Fisher精确性检验
相关性分析

  • Pearson相关

  • Spearman相关

  • Kendall's tau相关

  • 相关系数比较


聚类和因子分析

  • 系统聚类、快速聚类、层次聚类

  • 主成份分析


进阶能力: 回归、建模

  • 广义线性模型

  • 广义估计方程

  • 偏微分方程

  • 机器学习







从正态分布开始

从正态分布开始

正态分布(Normal distribution)/高斯分布(Gaussian distribution)
正态分布是一种连续型随机变量概率分布, 分布图是一条以均值为中心, 左右对称的钟形曲线。
若随机变量\(X\)服从一个平均数为\(\mu\) (mu) 、标准差为\(\sigma\) (sigma) 的正态分布，则记为：

\(X \sim N(\mu,\sigma^2)\)

其概率密度函数为:

\( f(x) = \frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \! \)

从正态分布开始

模拟正态分布抽样的频率直方图

从正态分布开始

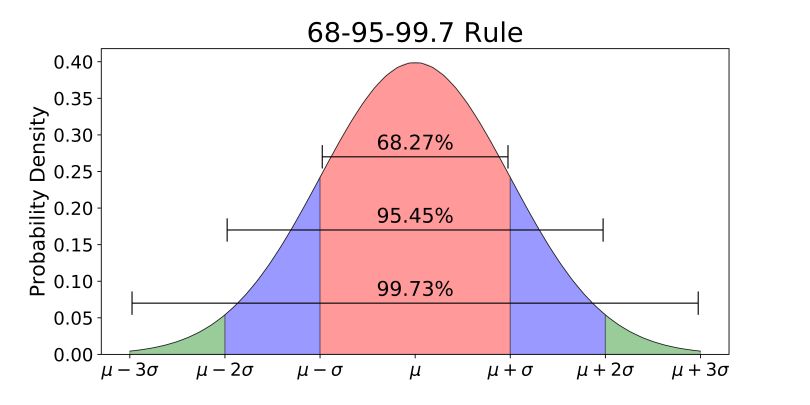
为什么正态分布这么重要?
简单

  • 只由两个统计量定义: 均值和标准差;

  • 分布曲线简单: 均值, 也是中位数, 也是众数;

  • 对称且稳定=>数学计算简单: 68-95-99.7 Rule

无处不在

  • 身高、体重;

  • 考试成绩;

  • 股票;

  • 测量误差;

  • 回归残差;

  • 大多数大自然中的变量;


WHY?

中心极限定理:大量随机变量的重复实验，其分布总和/均值将非常接近正态分布

应用广泛

  • A<=>B TEST:

    • T检验

    • Z检验

  • 回归模型;

  • 复杂分布的简化处理:

    • t分布

    • 二项分布

    • 泊松分布
最大熵属性:在不确定真实分布的情况下，选择给定限制下熵最大的概率分布。

从正态分布开始

为什么正态分布无处不在: 中心极限定理(Central Limit Theorem)







数据描述和数据清洗

数据描述

平均数mean

  • \( \bar{x} = \sum_{i=1}^{n}x_i / n \)

  • 更少受到随机因素的影响

  • 但更容易受到极端值的影响


中位数median

  • 排序后排名位于中间的数(如果有两个, 一般取平均值)

  • 不容易受到极端值的影响


众数mode 出现最多的数, 可以是多个, 如
        1,2,2,2,3,3,3

标准差sd、方差var

  • 标准差、方差: 描述数据离散程度 → 变量离期望值的距离;

  • 变异系数cv: 标准差/平均数 → 无量纲量


四分位数 quantile

  • [Q1:25%, Q2:50%, Q3:75%]

  • 四分位距IQR: Q3 - Q1


分布形态

  • 偏度 skew: 左偏, 右偏;

  • 峰度 kurtosis

数据描述



mean, median, mode, skew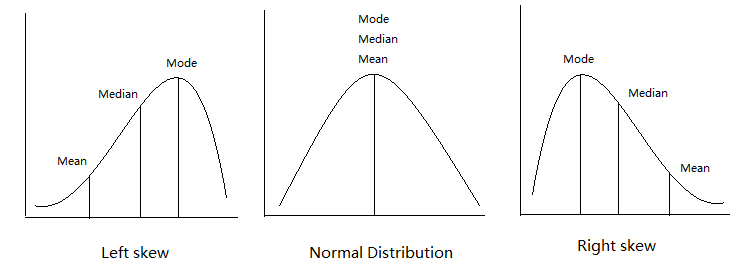
kurtosis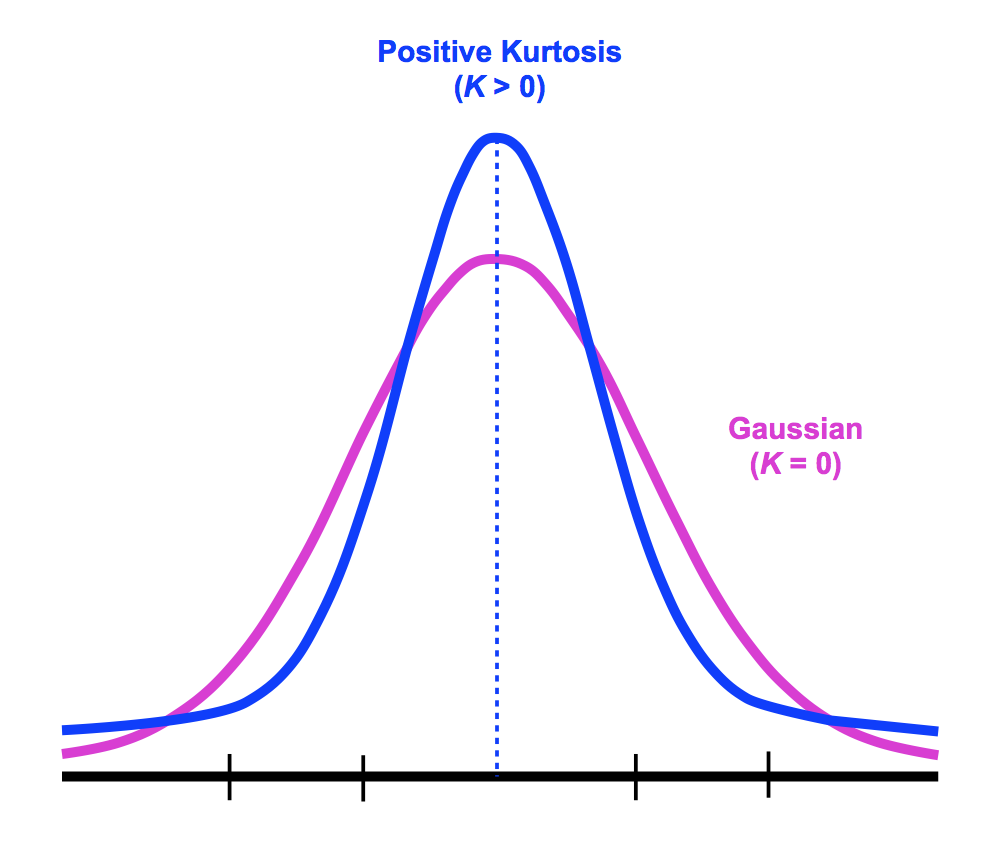

数据清洗-缺失值处理


 

性别职业月收入(元)
男霸道总裁NA
男外卖员10000
女网红直播NA
女当红明星NA
男鹅厂程序员25000
女生物公司销售9000
女小学教师6000
男硕士研究生0
 

材料干旱存活率株高籽粒淀粉含量千粒重
Rice10.520410
Rice20.4225NA
Rice30.32288
Rice4NANANANA
Rice50.72275
Rice6NA2459
Rice70.62395
Rice8NANANANA

数据清洗-缺失值处理


缺失值的产生的原因

  • 非专业调查

  • 数据丢失(存储不当、故障)

  • 敏感性问题(收入, 吸毒 ...)

  • 暂时无法获取的信息 (产品收益...)
数据缺失的类型

  • 完全随机缺失(missing completely random, MCAR): 缺失与数据特征和其他变量的取值无关, 实际应用中MCAR很少, 因此判断需要慎重;

  • 随机缺失(missing at random, MAR): 缺失与其他无缺失值的变量取值有关, 如统计小麦自然群体干旱条件下的产量;

  • 非随机缺失(missing at non-random, MANR): 缺失不仅和其他变量有关, 也和自身取值有关, 如统计家庭收入情况时, 有些高收入家庭不敢透露

数据清洗-缺失值处理

缺失值的处理策略

  • 不处理

  • 删除法: 按行删除; 按列删除; 按分析删除; 成对删除

  • 填补法: 用最可能的值来填补缺失值

    • 人工插补: 专业素养, 费时费力;

    • 统计填补: 根据简单的算法或规则进行填补, 易于操作, 但不考虑缺失值的变异性:

      • 平均值填补: 数值变量=>平均值; 离散变量=>最高频;

      • 条件平均值填补: 选取跟缺失对象特征类似的对象的平均值进行填补;

      • 热卡填补: 也叫邻近填补, 在整个数据集中搜索一个与缺失值最相似的值进行填补 如何定义相似标准? => 主观

      • K-means填补: 先根据距离函数判断与缺失材料最近的样本, 然后用样本的加权平均值估计缺失值 比较合理, 但分析大型数据时非常耗时

      • 复杂填补: 回归算法, EM算法, 多重填补

      • 其他方法: 学科特性的算法, 如遗传学的单倍型=>基因型填补

数据清洗-异常值处理


统计水稻籽粒颜色


    [黄, 黄, 白, 黄, 黑, 黑, 黄, 白, 白, 12cm, 锟斤拷]    

统计班中男性身高(cm)


    [2.29, 165.0, 166.9, 169.3, 170.9, 172.1, 173.4, 173.4, 174.0, 177.1, 209.1, 215.2, 1755]    

基因在群体中的表达量(FPKM)


     [0.1, 0.2, 0.1, 1.1, 1.5, 1.8, 3, 4, 10, 2000, 5000]     

SNP与表型的关联程度(P-value)


    [ 1, 0.9, 0.9, 0.8, 1, 0.5, 0.5, 0.3, 0.1, 0.0001, 1E-7, 1E-15 ]    

数据清洗-异常值处理



异常值的类型 异常值通常有两种情况：

  • 测量值随机波动的极度表现，即极值，它虽然与其余数据相差较远，但仍然处于统计上所允许的合理误差范围之内，这时的异常值称为局内值；

  • 与其余数据不属于同一个总体的异常值，称为局外值

数据清洗-异常值处理



异常值的检测方法

  • 专业判断: 最基础, 最可靠, 但实际研究中往往没有条件进行专业判断;

  • 图形法:

    • 直方图;

    • 箱线图;

    • QQ图;

    • ...

  • 统计描述法:

    • \( outlier ≈ \bar{X} ± 3*SD \)

  • 复杂算法: 分布检验, 回归拟合, 机器学习 ...

数据清洗-异常值处理


图形法: 直方图


在直方图上，位于图形两端，并远离均数的数值，提示可能存在异常

数据清洗-异常值处理


图形法: 箱线图


在箱线图上位于上下四分位数±1.5倍四分位间距的数值，提示可能存在异常

数据清洗-异常值处理


统计法: \( outlier ≈ \bar{X} ± 3*STD \)

julia> hh
210×2 DataFrame

 Row │ Gender  Height  
     │ String  Float64
─────┼─────────────────
   1 │ female  174.471
   2 │ female  173.414
   3 │ female  167.992
   4 │ male    168.214
   5 │ male    167.548
   6 │ female  170.572
   7 │ female  163.584
   8 │ female  172.297
  ⋮ │   ⋮        ⋮
 203 │ female  221.519
 204 │ male    222.97
 205 │ female  221.387
 206 │ female  218.243
 207 │ female  217.352
 208 │ male    221.358
 209 │ female  214.287
 210 │ female  220.17
 
# 定义函数
function is_outlier(x, mean, std)
    x >= (mean + 3 * std) || x <= (mean - 3* std)
end
# 计算X̄和STD
h_mean = mean(hh.Height)
h_std = std(hh.Height)
# 过滤
subset(hh, :Height => x -> is_outlier.(x, h_mean, h_std))
# 结果:
 Row │ Gender  Height  
     │ String  Float64
─────┼─────────────────
   1 │ female  223.006
   2 │ male    219.171
   3 │ female  221.519
   4 │ male    222.97
   5 │ female  221.387
   6 │ female  218.243
   7 │ female  217.352
   8 │ male    221.358
   9 │ female  214.287
  10 │ female  220.17

数据清洗-异常值处理


异常值处理中的注意事项

  • 异常值产生的原因不明之前，不应简单决定其取舍;

  • 通过图形法和统计描述法检测出的异常值，最好再从专业角度进行判断是否为真正的异常值;

  • 尽可能核对原始记录，如果确认数据有逻辑错误，又无法纠正，可直接删除;

    • 若数据无明显逻辑错误，可将数据删除前后各做一次分析，若结果不矛盾，则不予删除;

    • 若结果矛盾且需要删除数据时，必须给予充分合理的解释;

  • 若采用其他数值替换异常值，最好对替换前后的数据各做一次分析，并对结果进行比较

数据清洗-数据缩放转换



  • 规范化(Normalization)

  • 标准化(Standardization)

  • 归一化

  • 中心化(Zero-Centered)

  • 正态化(Normal transform)

  • 正则化

  • ...

数据清洗-数据缩放转换



为什么需要数据缩放转换?


消除量纲的影响 :
GDP(亿, 百亿) => 标准化

统一分析标准 :
发病率, 存活率, 病毒抗药性, 药物抗病性, ... => 正/负向化

符合统计模型假设 :
T-Test, 线性回归等要求符合正态分布 => 正态化

数据清洗-数据缩放转换


规范化(Normalization) :
将不同变化范围的值映射到相同的固定范围中，常见的是[0,1],此时亦称归一化

最常用方法: min-max normalization
\( X^{new} = \frac{X - X_{min}}{X_{max} - X_{min}}\)

去量纲化 , 尺度(scale)统一 , 不改变原排序 , 但不能处理异常值

数据清洗-数据缩放转换


标准化(Strandardization) :

将数据转换为均值为0, 标准差为1的新数据, 最常用的方法为

z-score标准化z-score normalization

\( X^{new} = \frac{X - μ}{δ}\)

去量纲化 , 不改变原排序 , 能处理异常值 , 尺度(scale)不统一

数据清洗-数据缩放转换


正态化(Normal transformation) :

将非正态分布的数据转换为正态/近似正态分布

常用转换方法:

  • 对数变换(Logarithmic transformation): 适用于对数正态分布,部分正偏态分布,均值与STD成比列的数据

  • 平方根变换(square root transformation): 适用于Possion分布, 轻度偏态分布的数据

  • 平方根反正弦变换(arcsine transformation): 适用于观察指标为比值或百分比的数据

  • 平方变换(square transformation): 适用于方差与均值成反比, 或左偏分布

  • 倒数变换(reciprocal transformation): 适用于数据两端波动较大, 或方差与均值的平方成正比, 且数值不能接近0

  • Box-Cox变换(Box-Cox transformation): 变换方式由可变参数λ决定, 对许多数据都适用, 应用广泛

  • 逆正态变换(Inverse normal transformation, INT): 将排序映射成正态分布

数据清洗-数据缩放转换


正态化(Normal transformation)

数据清洗-数据缩放转换


针对特定分析开发特定的标准化算法



RNA-Seq Reads Count的标准化

  • A: 比对到基因A的reads数

  • G: 比对到全基因组的reads数

  • \(L_A\): 基因A的长度

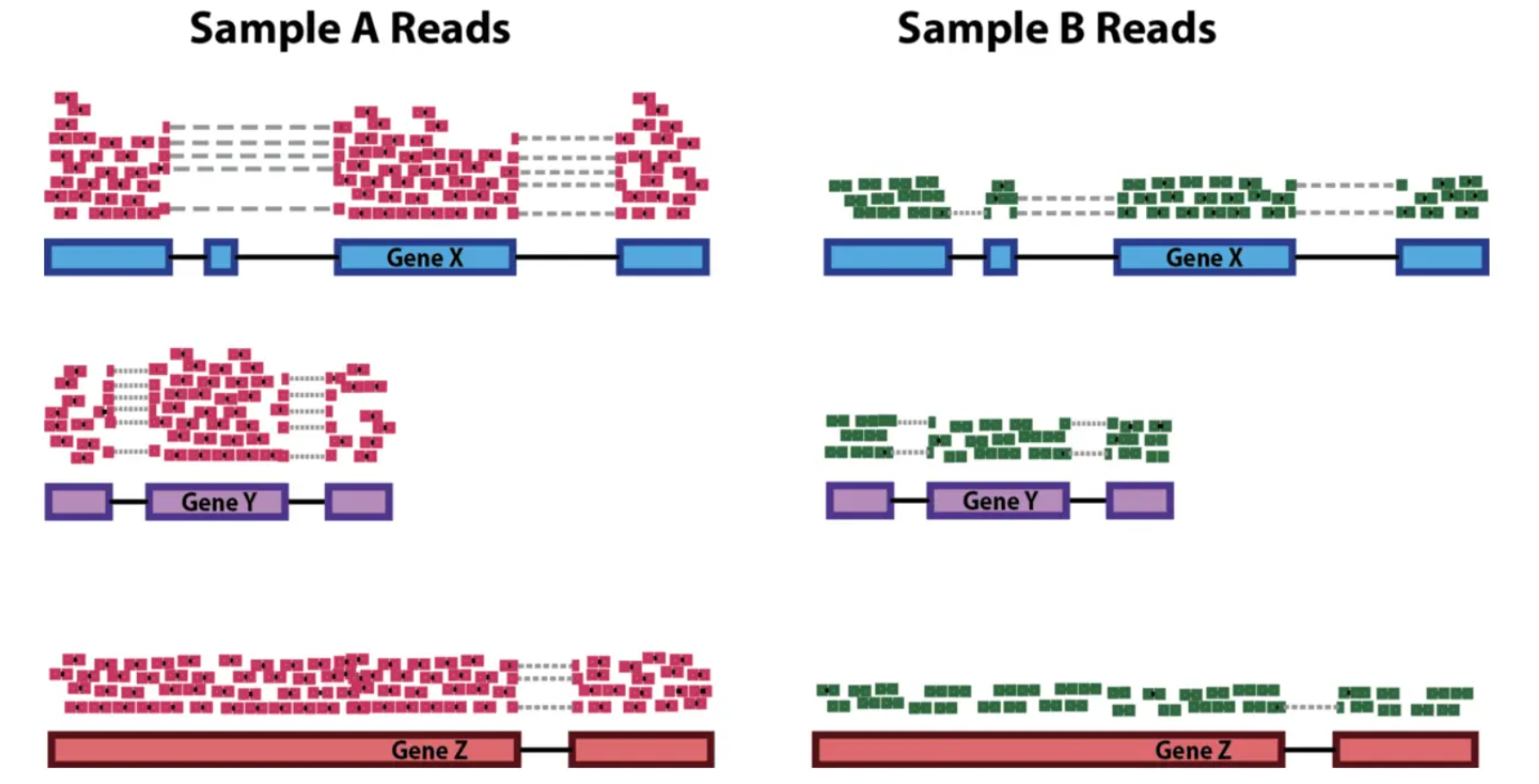\( CPM = \frac{A * 1E6}{G} \)

\( RPKM/FPKM = \frac{A * 1E6}{G * L_A / 1000} \)

\( TPM = \frac{RPK_A * 1E6}{\sum{(RPK_A)}} \quad where \quad RPK_A = \frac{A}{L_A / 1000}\)







差异分析: 以T-TEST为例

T-TEST


什么是T检验
t检验也称为Student t检验，它是一种使用假设检验来评估一个或两个总体均值的方法

t检验可用于评估:

  1. 某个组是否与已知值有差异

=>单样本 t 检验

  1. 两个组是否彼此有差异

=> 独立双样本 t 检验

  1. 成对测量值中是否存在显著差异

=> 成对或非独立样本 t 检验


  • 双尾检验 => \(H_0: μ_A = μ_B; H_a: μ_A ≠ μ_B\)
  • 单尾检验 => \(H_0: μ_A ≥ μ_B; H_a: μ_A < μ_B\)

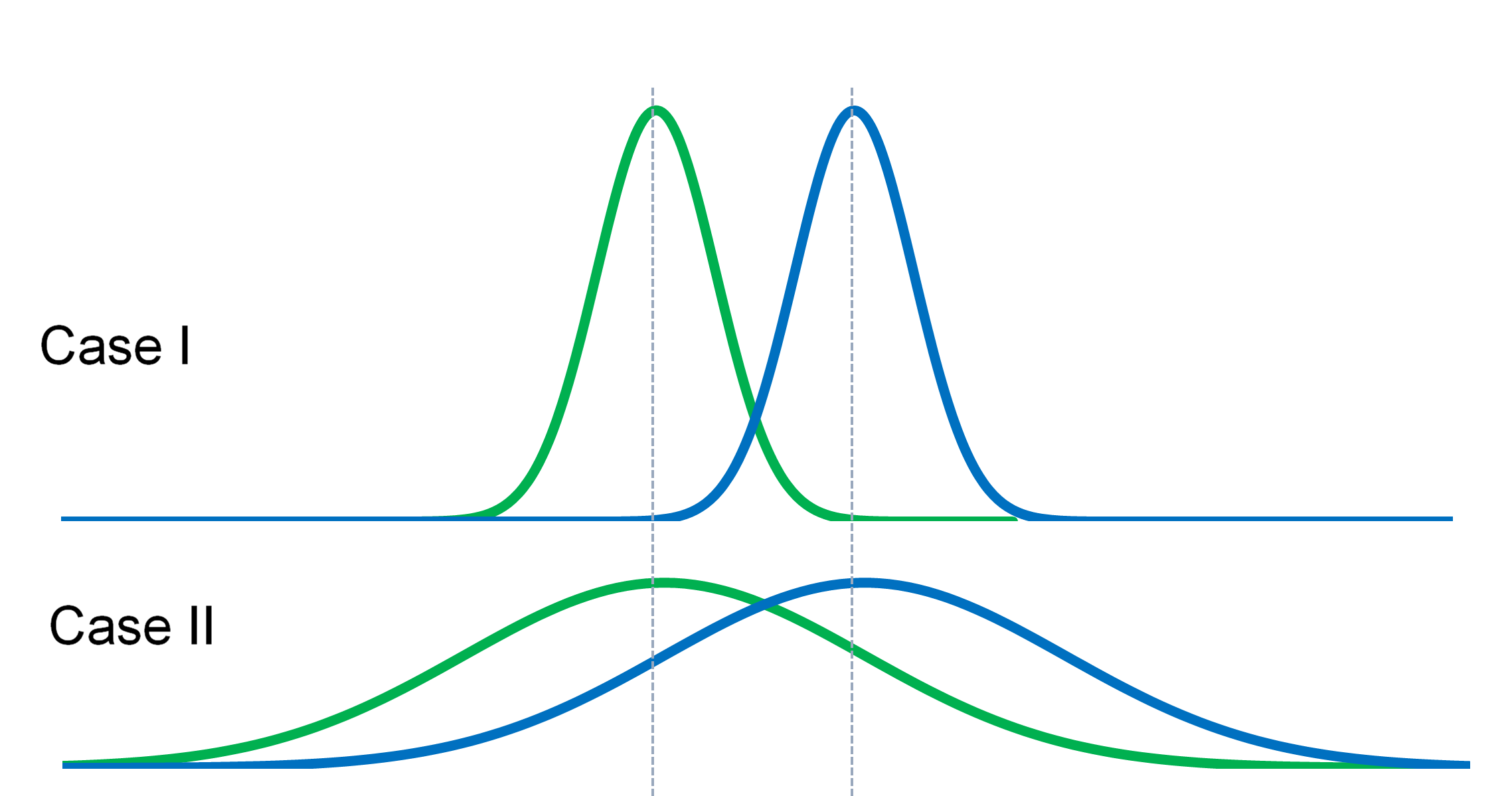    • T-TEST


    T-TEST的适用条件

    • 观察变量为连续变量;

    • 观察变量相互独立;

    • 观察变量不存在显著异常值;

    • 观察变量为(或近似为)正态分布;

    • 观察变量最多两组;

    T-TEST


    T-统计量的计算

    T统计量(以单样本T-Test为例)

    \(t = \frac{X̄ - μ}{s / \sqrt{n}}\)

    T分布


    其中ν为自由度

    拓展阅读: 什么是自由度

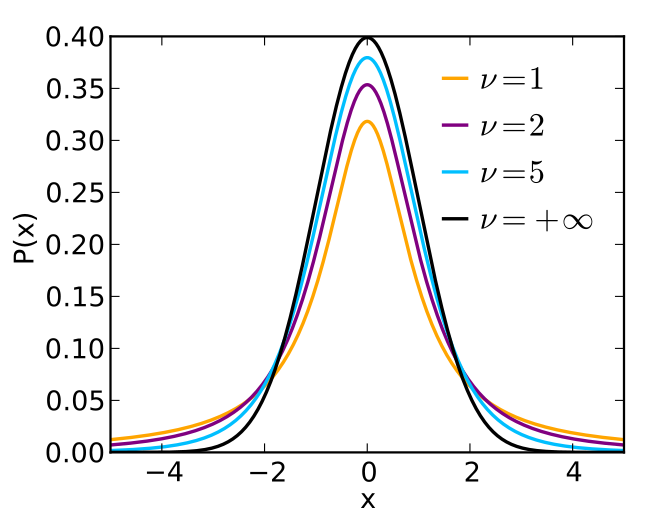
    参数检验和非参数检验方法

    拓展学习: 常用的参数检验和非参数检验方法对比

    推荐资源

    看见统计
    StatQuest
    可汗学院-统计学公开课